In the spring of 1979, I was a soon-to-be-graduated electrical engineer that needed a job. As with other young engineers, I started to look for work during my last semester of school and I got a few nibbles. The most intriguing of the nibbles was from Hewlett-Packard, known by all engineers as "HP." At that time, HP was considered a class engineering act and getting a job there would be perfect for someone with plenty of energy but little experience.
The first interview was on campus and was pretty interesting. HP was known for having a tough on-campus interview. They asked tough questions. The questions weren't necessarily technical – most were puzzles. Fortunately, I like puzzles!
The interview went well and they sent me a plane ticket to Ft. Collins, Colorado for an interview. Soon I was out in Colorado. It was the first time I had flown (excluding one quick flight on a Piper Cub when I was 7). It was also the first time I had stayed at a motel without my parents. It was a trip filled with firsts for the kid from small-town USA!
The interview ended up being a grueling six-hour puzzle-solving session. Once I got over my initial jitters, I relaxed and actually enjoyed the experience. It must have gone well because I received a job offer before I left the building.
During my interview, there was one problem that kept coming up. It turned out the problem had been the subject of much discussion within HP. The Fort Collins facility was filled with engineers who loved math puzzles, which made sense when you think about their interview process. If you hire based on the ability of people to work puzzles, you probably end up hiring people who are good at them.
The problem begins with a young engineer being handed a 1 F (Farad) capacitor that is charged to 10 V.
You are handed a 1 F capacitor charged to 10 V and two boxes containing uncharged capacitors: one box contains an uncharged 1 F capacitor and the other contains 1 million 1 µF capacitors. You can connect the capacitors from one box, one at a time, across the charged capacitor. Your job is to determine which box will allow you to discharge the voltage on the charged capacitor the most?
Consider the first box. You can think of a 1 F capacitor as one million 1 µF capacitors in parallel. When this capacitor is connected across the charged capacitor, the final voltage will be 5 V and every capacitor will have the same voltage. The following figure illustrates the situation.
Now consider the box of one million capacitors. The first small capacitor you apply will be charged to nearly 10 V because the capacitor being connected is so small compared to 1 F.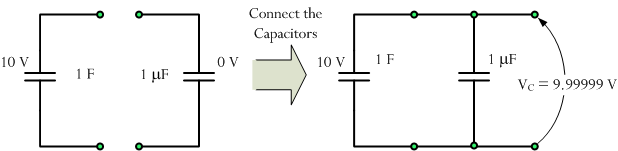
We can compute the voltage on the 1 F capacitor using the definition of capacitance. Let 
This equation can now be applied one million times to determine the final voltage. Of course, applying this equation one million times means that we will be close to the limit of the following equation. So let's go find the limit.
To simplify my notation, let 
When I looked at this equation, I realized that this was the equation for continuous compound interest. While in school, I had seen this limit and I was able to write down the answer directly.
So the answer to the question of whether to choose box one or two was clear ─ choose box 2 with one million 1 µF capacitors. The capacitors will end up charged as shown below.
My interviewer looked stunned. He asked how I knew this and I told him that I had seen the limit before. He looked dismayed and said that he would prefer to see a method that did not require a "miracle" of observation. Our interview time was then over and I had another interviewer to face. Later that day I would receive a job offer and would return to live in Ft. Collins a few months later.
When I arrived in Ft. Collins to start my job, one of my interviewers came up to me and asked if I could come up with a more satisfying solution (i.e. one that did not require identifying the series by inspection).
As I looked at the equation, I told my interviewer that l'Hôpital's rule could probably be applied. My interviewer said that l'Hôpital's rule did not apply to equations of this form. Fortunately, I had recently seen a professor solve a similar problem by applying l'Hôpital's rule's to the logarithm of this equation. It turned out that l'Hôpital's rule could be applied to the logarithm of this equation.
The interviewer looked at me with both happiness and dismay. He said that he had been working for months off and on trying to analytically come up with the limit. He also mentioned that my puzzle-solving ability was what motivated them to hire me.
Ever since then, I have fondly thought of this math puzzle. It is hard to believe that it got me my first real job!
Huh, must be different for different HP facilities. Oddly enough, I graduated in 1979 as well, but interviewed in, I think, Palo Alto, but I don't recall getting any puzzles to solve. It's all in the dim past now, since I haven't don't any real EE since about 1987.
Cheers
I was at the Ft. Collins facility. They were pretty big on puzzles. Lunch was occupied with chess and other board games. My wife still talks about all the card playing in the evening. Sounds like it was just the culture of that facility.
Just stumbled upon your blog and enjoy it! I've gone back through your archives and looked at all the entries, some of which I'll return to to read in more detail.
I was struck by the million capacitor problem and solved it by recalling that one definition of Euler's number is [(1 + 1/n)^n] in the limit as n becomes infinite. This is the same form as the denominator of the expression for the voltage remaining on the 1F cap. Therefore, in the limit as the number of caps gets very large and their values get correspondingly small, the lowest the remaining voltage can go is 1/e times the original voltage. (Of course, in this limit, it would take so long to do this that the self-time-constant of the original 1F cap would discharge it, so the practical answer is 0v!)
Here is an interesting question related to this one: How much energy is stored on the original 1F cap? If it is connected to a discharged 1F cap and the charge allowed to redistribute, what is the total energy finally stored on the two caps? Please explain any before-and-after difference.
By the way, I share your sense of loss at the death of Jim Williams. I think that while he probably did do app notes while he was at National Semiconductor, the ones which really brought him fame and admiration were all written for Linear Technology Corp. Jim will be hugely missed for his knowledge, insights, helpfulness, and humbleness.
Thank you for the comments. Let's take a look a your question about discharging one capacitor into another.
It turns out this question was also asked during my interview. It is a classic -- there is even a Youtube video that discusses it. This situation pits the law of energy conservation against the law of charge conservation. Of course, both laws hold, but the bookkeeping associated with the law of energy conservation is more difficult because so much energy is lost in the form of heat. Thus, it appears that the law of energy conservation is violated.
Couldn't find the Youtube video. Did find a lot of exploding capacitors, though! Apparently they love blowing up capacitors on Youtube.
Meant to mention that these two problems together beg the question of how much energy is stored in the million charged 1uFs and, added to 6.7668 joules remaining on the 1F, how does the total compare to the original 50 joules. This is a tougher problem because each small cap is charged to a different - though calculable - value. I haven't tackled that question yet; maybe you have.
Hi Anson,
I updated the Youtube link (I grabbed the wrong one). I haven't looked closely at the cap puzzle from an energy standpoint, but I will. It should make a good blog post. Thanks for the comment and question.
Mathscinotes
Hi, I realise that this post is rather old, but I stumbled across your blog while looking for information about lead acid battery gas production. That information was useful and I carried on looking through the rest of your posts. This one interested me as I also enjoy solving puzzles- and a very elegant answer came to mind quickly.
The first 1uF capacitor will reduce the charge on the 1F capacitor to 0.999999 of its previous value, and so will every other 1uF. So you can just raise 0.999999^999999, and multiply by the 10V initial charge to get 3.678796 V. Done!
Cheers,
Dan
Very nice way to look at it.
Mathscinotes
Great article...Spell check killed you... Its L'Hôpital's rule not hospital....lol 🙂 Really a great article 🙂 cheers
Thanks for the spelling help. I do depend on spell check pretty hard.
mathscinotes
I found my way here because I was looking to establish whether the discharge of one capacitor into another is exponential. Clearly, all simple RC ccts discharge exponentially but I don't quite see how the maths works through for two capacitors (one discharging into the other) in this arrangement.
To the Q posed, however, I have the following observation:-
Isn't the puzzle the same for a 1F cap discharging into two 0.5F caps of the same form?
That clearly shows that multiple caps take more charge away (because you are left with 2/3 of 2/3Q on the 1F cap). Three 0.33F caps would be 3/4 of 3/4 of 3/4 etc. That, surely deals with the Q originally posed, BUT proving that the final Q tends to Q/e would, I grant you, be a scale up!
To my question, is there a simple way of showing that the discharge is exponential or not?
Can anyone enlighten me?
Both forms (l'Hospital or l'Hôpital) are correct, e.g., see:
http://mathworld.wolfram.com/LHospitalsRule.html
The above Formulas are total crap!
All of you readers didn't notice?
Oh Jesus, is this possible - unbelievable!
1*10^6 is NOT infinity!
1*10^6 * 1µF = 1F is not (infinity * 1µF) = infinity F
correct Formula:
V(0)*C1 = V(k) * (C1 + k*C2) | k= 0...n
V(k)= (V(0) * C1) / (C1 + k*C2))
V(k)= V(0) * C1 / (C1 + k*C2)
V(k)= V(0) * 1F / (1F + 10E6*1eE-6)
V(k)= V(0) * 1 / 2
V(k)= 5V!
If YOUR Formula would be right, it would violate the conservation of electrical charge also. Doesn't this bother you?
One could ask: "Where have all the missing electrons gone?"
(10 Coulomb initially vs. 7,3576.. Coulomb ??)
Did they vaporize?
Sorry it took time for me to get to your comment -- I have been travelling. Your comment is different than I usually see because normally people observe that energy appears to not be conserved, but charge is. In the figure below, I show my demonstration that charge is conserved.
If you do a similar calculation for energy, you will see that energy appears to not be conserved – I will let you do the calculation. This is a well-known issue in charge sharing systems that has been understood for a long time. I refer you to the following EE lecture I selected from a number of options.
Hi,
as you censored my last mail, I will make it short.
Your Formula is wrong!
I've tested in EXCEL with successive 1000*1E-3F. And guess what - 5,0000V!
So it will be for 1E6 *1µF. Don't you think so?
Censor once more the facts
No guts...
Please see my comment to the original comment.
Test Comment.
Please see my response to the original comment.
Dear "Mathscinotes",
we were currently discussing about your capacitor theory and think that your theory is not right.
We think that your limit calculation is NOT right. With your calculations the laws of nature are reinvented. My engineering friend Axel already wrote you and we are waiting for an answer.
Please see my response to the original comment.