Quote of the Day
Science is not about what's true or what might be true, science is about what people with originally diverse viewpoints can be forced to believe by the weight of public evidence.
— Lee Smolin, theoretical physicist
Introduction

Figure 1: A view across a 20-km-wide
Spanish bay. The curvature of the Earth
hiding the base of the buildings on the far
shore. (Wikipedia)
I frequently hear people make statements that somehow do not seem right. Today, during a discussion of laser levels, the topic of required accuracy came up. I heard a contractor state:
Who cares if the laser level is accurate within an 1/16th of inch at 100 feet? The Earth curves away from a horizontal line by 1/8th of inch for every 100 feet of horizontal distance. The Earth's curvature will swamp out your instrument error in less than 100 feet.
The statement about the curvature of Earth got me thinking. How much does the Earth's surface deviate from a horizontal line over a distance of 100 feet? The contractor's number intuitively seemed wrong because the Earth is round and the deviation from horizontal should be a function of distance. A little math will give me the answer. For consistency's sake, I will perform all computations in US customary units.
Analysis
Figure 1 illustrates the situation and contains the derivation of both an exact and a approximate solution. The triangle formed by x, R + δ, and R is a right triangle, which means that the Pythagorean theorem can be used to produce an exact solution. In addition, a simple approximation for δ is also developed assuming R >> x and using a linear approximation for the square root. In Appendix A, I give examples of the computations in Mathcad.
Given the situation shown in Figure 1, we can compute the deviation from horizontal as follows.
| Eq. 1 |
where
- R is the radius of the Earth (3963.2 miles)
- x is the horizontal distance of interest (100 ft)
Conclusion
The contractor had stated that the curvature of the Earth causes level to deviate from horizontal by an 1/8th of an inch (125 thousandths of inch) for 100 feet of horizontal distance. The actual deviation is ~2.9 thousandths of an inch for 100 feet of horizontal distance, which is almost 45 times less than the contractor claimed. So it is meaningful to buy a laser level that is accurate to 1/16th of an inch over 100 feet, i.e. the laser level error is not swamped by the curvature of the Earth.
Why did the contractor make the claim that the Earth's curvature is 1/8th inch over 100 feet? He made a simple mistake. He did not understand that the deviation from horizontal for short distances is given by a square-law relationship, shown in Equation 2. In Equation 2, I include an approximation that is only valid when R is much greater than x, which is true in typical construction problems.
| Eq. 2 |
If we use Equation 1 or Equation 2 to calculate the deviation from horizontal at 1 mile, we get 8 inches. This value is quoted in a number of references on surveying (e.g. here is one, here is another, yet another). What the contractor did was erroneously assume that the deviation varied linearly with distance, which would mean that a deviation of 8 inches at 1 mile is equivalent to an 1/8th of inch at 100 feet.
For those of you who may be interested in the related question of the error in horizontal distances caused by living on a spherical planet, see this blog post.
Aside: Here is an interesting discussion that references this web page.
Appendix A: Computation Examples
Figure 2 shows a few computation examples. Normally, I let Mathcad do the unit conversion, but I do show one example with explicit unit conversion.



hello, I was confused by your quotient because you state the distance in kilometres and the elevation in feet, and then at the end you quote the distance in miles and the elevation in inches. this is crazy and confusing! Using 4 units of measurement with only one equation, when there should only be one. it doesn't say anything about the conversion in the equation, so I figure it could be metric, then when I use metric in the calculation, the result is different from what you say. I will actually have to look on another website! for the solution! Cheers! happy Christmas!
Dimensional analysis can help you keep things straight. I have added a small appendix that illustrates the calculations. Normally, I let my computer algebra system do the unit conversions for me, so I never actually worry about them. In the appendix, I illustrate how to perform the unit conversion. I hope that helps.
Merry Christmas.
Mathscinotes
it's called deceptional analysis
The math and science is completely flawed! its based on pure assumption! its embarrasing that people use it all. This is why the people can call it flat because by its own measure you need to be under the sea leveI to view anything at even a few miles away. I know how to get accurate measurements using basic free tools and gadgets. Why not add a climate change detector, or Bill Nye or a Luna module whilst you at it. Even if you are a die hard believer in what you see and believe, science and math is not proven! its called theory and scientific exploration for a reason. Good luck! oh covid is a hoax!
I like your web page but I have a question. Since it's been over 40 years since I took algebra could you explain equation 2? When I use smaller numbers, like 3 for x, 4 for r I get different answers between the first step & the second step. 1 for the first step & 1.25 for the second step. Thanks
My article was not clear on the approximation and I have added some explanatory text. The approximation is only valid when R is much much bigger than x. This is true when R is the radius of the Earth and x is a typical construction distance. The approximation fails when when R and x are similar in size.
Hopefully, my clarification in the text will help. I am so used to doing these sorts of approximations that I do not even notice when I do them -- very bad habit.
Mathscinotes
Seriously? and you are to be considered an expert with an opinion to be considered?
Hi, Thanks for your calculation for the vertical error. I am however interested in figuring out how much the distance between two points vary with curvature of earth (as opposed to just using trigonometry). Could you help me in figuring this calculation out? Thanks
Hi Hanna,
I would like to try to help, but I do not completely understand your question. Are you trying to determine the distance between two points on the Earth's surface? If so, I can help. Generally distances on the Earth's surface are expressed in terms of the great circle distance. There are numerous web sites that address this calculation, like this one. If you are interested in a proof of the formula used on this web page, see this reference. If you decide that you need an Excel version of the calculation and are having trouble putting it together, I can pull something together in less than a minute.
If you have a different question, just give me a bit more detailed version of your question and I will try to help.
mathscinotes
Hi. For some reason I never saw your reply. Thanks for getting back to me. I am observing animals from a 93-96m high sea cliff (tidal variation) with a theodolite. I get angles from reference point that allow me to calculate the (diagonal) distance of the animal in the water from the theodolite on the cliff top. As I know the height at that moment, I can easily calculate the horizontal distance from the theodolite to the animal. However I would like to know what is the actual distance of the animal from the foot of the cliff, if the curvature of the earth is taken into account. I have tried using the moveable typescript calculations but am not sure if I can do it correctly. Assuming the angle from is 45degrees
Hi Hanna,
Let's take a quick look and see if I am thinking of your problem correctly. To keep things very simple, let's assume that your theodolite is 100 m above the ocean and you are observing something in the water at a 45 °C angle. Using "flat Earth" methods, your subject is 100 m away -- correct? Let's work the same problem and determine the arc length of your subject from a point directly below your theodolite.
Here is my drawing that illustrates this situation.


I can convert this situation into a geometry problem as shown in the following figure.
I can analyze this geometry as shown below.

As you would expect, the arc distance is not much different than the distance you would compute using simple angles.
Is this what you were looking for? I can put it into Excel if you want to play with it.
Mathscinotes
Why on a clear calm day can i take a perfect picture of chicago from lake mi.In michigan?200 plus miles straight across.
Lake Michigan is no 200 miles across, just 38 from Michigan City, IN to Chicago, yet bottom half of Willis (Sears) tower is cut off from view by the ~900ft of curvature at 38 miles. Only the tallest buildings in Chicago are visible at this distance.
The entire buildings are visible
There have been many direct line of sight observations taken with high def, super zoom cameras showing the Chicago skyline from the shore up from points up on Lake Michigan from 50-62 miles away. At 62 miles away, there should be 2,400 feet of curvature blocking this view but there isn't. When one such photo was aired on the local Mi news, they said it was a mirage which made no sense since all mirages are inverted. The next falsehood purported was due to refraction. I would insert a few photo but you can't on here.
The images can be inverted or not. I have seen both. Here are examples I found from a quick search. I cannot comment on the Chicago story as I am not familiar with it.
Inverted Ship Image
Source: tltichy
Non-Inverted Ship Image
Source: By Timpaananen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=20987355
Yeah you can't fake the earth being a globe anymore. We are all waking up to it. I leave near the ocean, Have been a surfing photographer for over 35 years. I point my video camera on a clear day at the Santa Barbara Channel Islands from the beach and I can see the beach in front of the mountains. I can see the beach. Yet the island is 28 miles from shore and if the horizon drops 8" for every mile, then what I am looking at should be 20 ft below the horizon. How is it can see the sand on the beach? Because the earth is flat. Wake uP sheeple and you fake scientist that actually know the truth, your day is coming for this carrying on this lie.
The reason why you can see the beach on a clear day is because of the Fata Morgana effect. This is when it is clear and calm there is a layer of warmer air above the air cooled by the water. This causes some of the light to refract allowing you to see objects past the horizon. If the earth was flat you would be able to see europe from boston with a telescope.
The next time the weather channel says there is infinite visibility, then yes, you would be able to see Europe from Boston. What am I missing here?
truth seeker Wake up and you will know the actual truth, your day is coming for this carrying on your lies of thinking the world is flat.
Pingback: Whale Math | Math Encounters Blog
Je peux vous dire que c'est continuellement du bonheur de passer sur
votre blog
Hello:
I am trying to check and see if my math is correct. I found your article and wanted to see if I was on the right track.
I am trying to figure out the curvature of the earth based on the distance...
Thanks
James
Miles Squared X 8 Inches= Inches Of Curvature
6 Miles X 6 (Squared) = 36 x 8 = 288 Inches
288 / 12 = 24 Feet
Miles Curvature Drop
1 8 Inches
2 32 Inches
3 6 Feet
4 10 Feet
5 16 Feet
6 24 Feet
7 32 Feet
8 42 Feet
9 54 Feet
10 66 Feet
20 266 Feet
30 600 Feet
40 1,066 Feet
50 1,666 Feet
60 2,400 Feet
70 3,266 Feet
80 4,266 Feet
90 5,400 Feet
100 6,666 Feet
120 9,600 Feet
Close, it's slightly more than 8" per mile² so as you add more and more miles your answer drifts from the actual value (assuming a prefect sphere). Why not just use the exact equation instead of an approximate though?
Beyond that - there are a couple of very serious issues with this that people often fall into...
#1 the largest effect that makes this table almost COMPLETELY irrelevant is that it doesn't take into account the VERY SIGNIFICANT contribution from the refraction of light. When talking about 100 miles over the ocean this table will be off by DOZENS OF MILES in terms of where the ACTUAL APPARENT HORIZON appears. Thanks to refraction you can see much, much further "around" the ocean than most people seem to understand. The net effect of refraction is to make the appear a fraction larger around than it actually is. The *nominal* value for this is 1/7th of the curvature of Earth -- So if you want to get an approximate value for refraction you can use R*(7/6) to adjust for refraction. However, the actual value can be significantly GREATER than 1/7 - especially in sea level, warm, humid conditions like you expect to find around tropical islands. Try the same trick up around Greenland on a cold, dry day at higher altitudes and you'll find a significantly smaller effect.
The refraction of light can vary from very slight effects to the extreme end of COMPLETELY BENDING LIGHT AROUND THE GLOBE -- in fact, when you view a mirage the refraction is so extremely the light is bending upwards! The refraction of light in humid, dense air -- especially right above a body of water -- is very severe. The exact effect IS ALMOST IMPOSSIBLE TO CALCULATE because you almost never know, with sufficient precision, the exact structure of every molecule of air between you and the object viewed -- especially at a great distance. However, you can get a *pretty good* approximate if you control for the primary factors: frequency of the light, the density of the atmosphere, the gradient of density, the humidity, temperature, and CO2 content of the atmosphere.
If you want to account for all the conditions to the best of our ability then what you want to do is look up Ciddor and Edlen - these formulas are EXTREMELY complex - so good luck with that! But, thanks to our tax dollars, there is a web-based calculator! http://emtoolbox.nist.gov/Wavelength/Ciddor.asp
But the results are only as good as the input data -- if you make up data (oh, it was probably 30C on that day) then you get the wrong results.
What we do know for certain is that the effects of refraction, especially over the ocean, often allow you to see FAR FURTHER around the globe than you possibly could without refraction. Failing to account for this refraction is EXACTLY the error made in the https://en.wikipedia.org/wiki/Bedford_Level_experiment -- the view at 8" over the water was VASTLY different from the few a few feet higher. It actually LOOKED flat at 8" elevation - that's how strong the refraction was due to humidity differences.
And people were RIGHT to question this -- "hey it REALLY LOOKS flat" but the error was in failing to accept new information that clearly disproved the flat hypothesis.
I've reviewed DOZENS of images where people are ASTONISHED that you can see a distant island where the NAIVE equation says you shouldn't be able to see it -- in every case when you account for even AVERAGE refraction you get a curvature value that is RIGHT where it should be.
#2 the Earth is SLIGHTLY oblate, not perfectly sphere so actual values would be a TINY margin off from these values. You need to use a model for the Shape of the Earth that takes this into account if you want to get more exact values and those values will ONLY be accurate for a specific latitude, longitude, and viewing angle & distance (and doing so requires integration over the surface).
HOWEVER -- This is NOT a hugely significant effect. Why?
Well, the Equatorial radius is 6,378.1 km while the Polar radius is 6,356.8 km -- that's not a huge distance. In fact, in MOST pictures of the earth you are talking about A FEW PIXELS of difference - that's less than the error for most resolutions. The exception for this is in extremely high resolution images (11000x11000) such as from the Himawari 8 (Japanese weather sat) where you can see the Earth is about 38 pixels wider than it is high (about 1/100" on my screen). I cannot SEE the difference from a sphere because this is such a SMALL % difference, but I CAN measure the exact pixels and also calculated the expected values and they are in agreement to within the precision of the data I have.
#3 Even once you take the above into account you STILL haven't taken into account the shape of the landmasses and the Tides, which will affect the shape of the water you are viewing over.
#4 people forget they are viewing most of this slope almost edge-on, this has so many distorting effects on viewing I cannot even list them all.
But what I can tell you is that the culmination of everything is that YOU CANNOT visually discern the curvature of the earth below about 30,000 feet and even then you need a very wide angle of view and, to make matters worse, ALL LENSES, including your eyes, introduce barrel distortions and are unreliable unless you have the EXACT equations for that lens and know the exact lat, long, altitude, & angle.
This error goes for people posting images of rounded Earths as well -- MOST of the curvature you see in ANY picture below the ISS is barrel distortion. Even at very high altitudes you are only seeing a few hundreds of miles of a globe that is almost 8000 MILES across. Even 100,000 feet is just BARELY off the surface of this monster. People seem to have no idea of the scale of things.
41,850,000 feet wide and you are 100,000 feet up? Come on!
This is the best article I have seen on that side of the question.
Visually discerning the curvature of the Earth
http://thulescientific.com/Lynch%20Curvature%202008.pdf
Go here if you want to see what it REALLY looks like (from 35,800 km! up)
http://himawari8.nict.go.jp/
This beast takes 11000x11000 images in 16 DIFFERENT frequency bands (which includes visual, near-IR, and IR) and gives astonishing clarity.
You can watch a movie of an entire month of data (~4000 images)
"-- in every case when you account for even AVERAGE refraction you get a curvature value that is RIGHT where it should be."
There is no "standard refraction", since the amount of the water molecules in the air is always changing day by day and moment by moment, and therefore the Metabunk Standard Refraction Calculator is BS. Mostly you experiencing a lot of refraction between the camera and target when filming from very far away. But just wait for the good day, and you will see that the refraction was causing the target being magnified, also DOWNWARDS, and therefore, if you see something being behind curvy water, then it is just an illusion since the magnifying is bending the VISIBLE lower part downwards. I have spent hundreds of hours filming far away objects very close the sea level. In my link underneath is one example with four different photos taken of the same island and lighthouse from a distance of 18,84 km, while the eye level is 0,94 meters above sea level. The top of the lighthouse is 40 meters above sea level (no need to take tides into account since its always nearly zero here in Finland. Every one of the photos is taken from the same distance, same place, same height, with the same camera and with same optical zoom (x83). Watch it and think for yourself and you will understand that the refraction is causing illusions of a curvy water especially in the two upper photos which the last photo is proving wrong:
http://tietopiste.com/wp-content/uploads/2017/09/majakka-eri-olosuhteissa.jpg
In the last photo, you can see the horizon being BEHIND the island and that's why we know it is not a mirage, and also because of two other things which I will not tell now since this posting is already too long.
I am taking big issue with this article.
Here you said there is a 2.9 thousandths of an inch curvature for each 100 feet of horizontal distance.....(heheh).
I hate imperial so please allow me to convert it to metric.
0.07366 mm = 30.480m
Multiply all of this up by 1000 =
73mm fall for every 30,000km. Are you mad? One would have nearly gone around the whole circumference by then - for what a 73mm fall in curve? When the diamerter is ?
Those that come up with 8inches a mile are much closer to the truth.
30 meters times 1000 is not 30,000km, it's 30,000 meters.
Kevin McMillen
km or m? Exactly! It should've alerted one. Hence the 1000$ lost for each greenback!
No, the author is not mad, but you need to check your maths. You made a very significant error, and then proceeded to make a conclusion based on that error.
Correction: "When the diameter is"........12,742km? The observor has curved through thousands of km not less than 1 centremeter you madman.
I can assure you the author is not mad. You, on the other hand, I am not so sure about. You take 1 number from the post, and then completely miss the point of the post (was that deliberate?) and abuse the number in the most absolutely ridiculous way possible to draw a completely wrong conclusion. Then you delude yourself into thinking that is evidence the author is mad???
Your most amusing part is that you seem to suggest that "8 inches a mile" is about correct. You should try applying your same abuse to this number, and you will again assume the author is mad. Trust me, the author is not the madman.
If you want to understand this, you should read the section titled "Conclusion" and pay particular attention to "square-law relationship" and "What the contractor did was erroneously assume that the deviation varied linearly with distance". A mistake you made as well.
Thank you. Very nicely put.
mathscinotes
I think 18 miles is level at a 6' height??, on a perfect sphere, 131,477,280 ft.
So, this begs the question: At what point would the curvature of the earth "swamp out" the instrument error?
This is a good question and it all comes down to how you define "swamped". Let's assume that a measurement becomes useless when the error of the instrument equals the curvature of the Earth. My laser level has an error of 1/8 inch per 100 yards (i.e. an angular error). With respect to curvature, this means that the instrument is useful out to about 484 yards. The calculations are as shown below.
so now "swamped" is relative to the explanation? Kind of like "relativity" is relevant to the idea of gravity? it is fluid and never to be defined the same by any "expert" i.e. the goal post can always be moved to meet the purpose
The earth is flat and if you would do you maths and just natural obervations you would feel that it is not spinning and always raise to eye level no matter how high you go. If you feel it spinning please go and see your doctor.:-)
How is it that you people are so incredibly stupid?
...How is it that you people are so incredibly stupid?...
This question isn't beneficial and grammatically; it is confusing.
Your comment is like telling a child they made a mistake in their math homework.
You need to be precise if you want the child to learn. If you desire to feel superior, then throw away, and uninformed statements will display arrogance.
Lol, if you ever look at boats on the coast, you will change your mind.
Thank you Juan,
finally the correct answer! Whether you use 8" per mile squared or 6.5 " per mile squared... you still shouldn't see the statue of liberty from 60 miles, or the NYC and Philly skylines from 60 miles....
Use your heads people, test for yourself! If something disappears "over the horizon" (ship, for example) then how come you can see it again if you use binoculars? Impossible if the earth were really curved!
tragedy of science – the slaying of a beautiful hypothesis by an ugly fact.
Huxley
Just a matter of time before a flat-Earther wandered in.
Sailboat going gradually beyond and below the horizon: https://www.youtube.com/watch?v=7nUFLLUahSI
Large schooner disappears behind the horizon -- from the hull upward: https://www.youtube.com/watch?t=35&v=dV0h68YU0iQ
High and low observation of off-shore island: https://www.youtube.com/watch?v=bco_p4V7-QU
Clear demonstration of Earth's curvature on the Thames River, (skip to 5:00 to get to the beef):
https://www.youtube.com/watch?v=jRdgnj17FHQ
Base of buildings blocked from view by the water's convex curvature:
https://en.wikipedia.org/wiki/Horizon#/media/File:Horizon,_Valencia_%28Spain%29.JPG
Your reference material is excellent! Thank you very much.
mathscinotes
Malvarrosa Beach, Valencia
https://commons.wikimedia.org/wiki/File:Horizon,_Valencia_(Spain).JPG
1. Focal length 72mm of camera
2. People in the sea in reasonable in focus
3. Sea level ???? who knows
The focal length alone can create this effect.
Height above sea level looks to be about 6 foot.
Good illusion, well done.
If a ship is behind the horizon, no amount of zoom can bring it back into view. This should be painfully obvious. You're making the same mistake that many flat earthers continue to make. Just because a ship is too far away to see with the naked eye doesn't mean it's behind the horizon. A ship that's traveled beyond the limits of our vision, and a ship that's hidden by the horizon, are 2 very different things. And despite the number of times we've explained this, it apparently has failed to sink in. I can pretty much guarantee that the ships you zoom in on aren't behind the horizon to begin with. And it's this kind of misinformation that convinces people they're 100% correct. You people are completely oblivious to this.
Go buy a Nikon P1000 camera, go to the beach, and prove to yourself that one cannot bring a boat back into view.
Optics are outpacing lies. Take a go pro camera without a fish eye lens and attach it to a weather balloon. The horizon never falls and the sun’s reflection can be seen glistening across the ocean.
All of this cannot be achieved on a Freemason’s spinning ball all adds to 666 theory.
Have a nice day. From a guy who owns property and disagrees with surveying methods today.
Doug
When you can zoom your dumb Nikon and see the sun at 2 a.m. get back to us.
you globe folks always get butt hurt and respond like a child when you can't further your argument ... very small mind indeed
Juan - Go to a playground. Get on a merry go round. Have someone you trust give you a push so gentle that the playground equipment spins at the rate of one rotation per 24 hours. If you feel the movement, please do go see the Dr. Then revisit your comments and report back, if you would.
But aren’t we spinning at over one thousand miles per hour? I think I would feel THAT!
Would you feel that? Just how fast is the earth spinning?
Take a basketball, at noon start spinning it so that tomorrow at noon you've made one complete turn. Is that fast?
Kevin McMillen
Kevin, if you reduced the size of the earth to a baseball then you would have to scale the distance from the sun. The baseball would need to be on a length of string about 8,000 miles long. It would be moving very quickly to cover that ground in 24hrs.
Rocco, the string length and baseball size you suggest have a lot to do with the earth moving 365 days "around" the sun, and nothing to do with the earth's 24 hour spin on its axes. The latter is the spin under discussion.
The radii in the two comparisons are several orders of magnitude different. Acceleration is v^2/R. For the radius of the Earth, the acceleration will be 10s of thousandths less than a merry go round, for the same speed at the circumference of the circles.
Get a cheap analog clock. Remove the minute hand and second hand.
Sit and watch the hour hand move around the entire clock -TWICE. I suggest you can't detect the movement, but I could be wrong.
If you imagine the clock balancing flat on top of a basketball, you may understand that the hour hand is emulating the earth's rotation. The analog clock's hour hand is the analogy of the sun's apparent movement, even though it is the earth, but it is hard to detect since you are also moving.
Sit in a car in a wide-open space. Cover all the windows except the side one you are looking out. Have someone move an object slowly past the window. You cannot determine if it was the object or the vehicle moving because you are enclosed inside the experiment.
Final experiment. Sitting in a 60 mile an hour train on a long stretch of straight railway and the curtains drawn, you do not feel like you are moving as you can walk around inside the train.
600 mile an hour plane is the same thing. I hope I have been helpful.
You always find plumb to the center of the earth at whatever point your at on earth. All so let's say you were building a skyway from newYork to France. you would always stay x amount of feet above sea level bieng your reference benchmarks would always be right in front of you the (ocean surface) it would curve naturally with the earth. Railroads, roads are biult the same way. The benchmarks given to builders are close enough together so they don't have to account for curvature. Example : you could not use a fixed benchmark above sea level as a reference for grade at one point and the keep using that benchmark for the length of the railroad hypotheticly. Even if you had a laser thet was flawless and high enough off of grade to not be unstructed in anyway. your grades would start to become too high.
This is a false statement. Railroads are built level. You say you couldn't use the same benchmark to build hundreds of miles of track yet every airplane on earth uses "sea level" as the reference point for their altitude. Why isn't it called "sea curve"? I would recommend reading "Terra Firma" by David Wardlow Scott he does a fantastic job explaining this and many other proofs that we absolutely do not live on a giant spinning ball flying through space.
Sorry jackass, but aircraft do not use sea level as an altitude reference point for their altitude- the instruments ( among other things) use air pressure
You flat earthers are fucktards
There you go showing your true colors. Sad
There goes the small minded ego firing off insults because someone sees something different then him in all of his immense knowledge...you are pathetic and thusly disqualified from having a worthy opinion
Railroads and highways are built based upon elevation, not level. The curve of the earth is too insignificant. In 200 feet the curve is only about 1/85th of an inch.
Kevin McMillen
pseudoscience at its best! you always seem to have an excuse.......
contrary to nature ...
+water does not 'bunch up' at one end of the pond or lake..
+grammar school observations show that water is AlwAYs self leveling
+gyroscopes do NOT 'rotate' with the imaginary 'spin' of the plane(t) any more than 'day becomes night' 6 months from now as we rotate around a sun that is allegedly 93 million miles away
+infrared light does not 'refract' AND the Military IR Scopes can see 40 plus miles... but the plane(t) curve is 8 in per mile squared... ??
Try working out accurate targeting trajectories for long range artillery without accounting for earth's curvature. It's baked into the math. If it was wrong artillery would be useless.
Could you please figure the curvature using 1 mile. Math has never been my forte
This link lists the curvature at 1 mile as 8 inches. If you need to actually need to see calculations, just send me another note.
mathscinotes
I recommend this formula for "drop off at distance d" assuming a perfect sphere (note: assumes d < R)
√[R² + d²] - R
For your case, you can plus this right into WolframAlpha:
√[(Earth average radius)² + (1 mile)²] - (Earth average radius) to inches
http://www.wolframalpha.com/input/?i=%E2%88%9A%5B(Earth+average+radius)%C2%B2+%2B+(1+mile)%C2%B2%5D+-+(Earth+average+radius)+to+inches
Which is ~8.0065 inches -- so DO NOT trust 8" d² for larger values, you gotta use more precise numbers or your error accumulates.
To give a numerical example, using mean radius of Earth in this case, still at 1 mile:
√[(3958.7613)² + (1)²] - (3958.7613) ~ 0.0001263 miles ~ 8.002368"
So as you can see the exact value you use for radius of Earth matters and that varies based on where you actually are - the Earth isn't a perfect sphere, it's an oblate spheroid: https://en.wikipedia.org/wiki/Earth_radius
So at 100 miles that is 1.263 miles drop off.
This doesn't take into account significant affects of refraction of light for visibility however. I've posted in another comment about that:
https://mathscinotes.com/2010/11/straight-level-and-the-curvature-of-the-earth/#comment-28337
Here is my analysis of where 8" miles squared comes from (it is an approximation and it's not very accurate for distances > 100 miles) and why it's wrong:
http://flatearthinsanity.blogspot.com/2016/08/flat-earth-follies-how-to-derive-8-per.html
and the CORRECT formulas to be using take into account the viewer height:
http://flatearthinsanity.blogspot.com/2016/07/derivation-for-height-of-distant.html
Greetings,
I am a navigator and I use geographic ranging to calculate line of sight from an object with a known height to its line of sight horizon point. I use 1.169 times the square root of the height. Simply example: 1.169 x Square root of 100 equals 11.69 nautical miles to the point of horizon,
As I read Nathaniel Bowditch, the generally accepted master of navigational mathematics, I find he seems to use 1.146 instead of 1.169.
I am not sure why the accepted math taught today says to use 1.169.
SO I did some thinking.....Could the variation between Bowditch's math and the modern math have anything to do with the 14 mile difference between the polar radius and the equatorial radius?
Lastly, how did we come to use 1.169?
Thank you very much for any insight you would provide
Respectfully
Chris
Hi Captain,
It is quite likely that both Bowditch and the modern result are correct – it depends on the air conditions! First, I have looked at how to compute the distance to the horizon on this post, which uses metric units. I will convert to your units for this response.
If I ignore refraction, the distance to the horizon is given by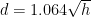 , where d is the horizon distance in nautical miles and h is the height of the observer's eye in ft. To add refraction, I need to make an assumption on the rate of air temperature change with altitude – a parameter known as the lapse rate. If I assume 11.3°C/km (common), the horizon distance is given by
, where d is the horizon distance in nautical miles and h is the height of the observer's eye in ft. To add refraction, I need to make an assumption on the rate of air temperature change with altitude – a parameter known as the lapse rate. If I assume 11.3°C/km (common), the horizon distance is given by  . If I assume another lapse rate, I can get 1.169 for a leading coefficient. Yet another lapse rate and I get 1.141 for a leading coefficient.
. If I assume another lapse rate, I can get 1.169 for a leading coefficient. Yet another lapse rate and I get 1.141 for a leading coefficient.
mathscinotes
Why is the drop measured from an angle from the center of the Earth rather than straight down from the horizontal/tangent(x)? For example, if I go ~4000 miles along x, I should show a ~4000 mile drop down from x. There seems to be a separate equation that perhaps doesn't use the Pythagorean theorem--can you show it? And if so, as 1) drop per movement along the horizontal and 2) drop per movement along the circumference.
Analysis, such Machinations, sheesh.
Try this approach with the given right triangle.
R^2 + X^2 = (R+delta)^2 – where R = 3963.2 mi. and X = 0.0185 mi. (or 100 ft)
15,706,954.24 + .00034 = 15,706,954.24034
√15,706,954.24034 = 3963.2 mi.
In other words, 100 feet will not demonstrate a visually noticeable difference.
And if you want to know delta (though why you’d want to know it I’m not sure as it is not necessary to the solution) it is √(15,706,954.24 - .00034) miles.
Or you could consider the distances used in the Bedford Level Experiment (https://en.wikipedia.org/wiki/Bedford_Level_experiment), in which Alfred Russell Wallace, co-discoverer of Natural Selection, participated.
Ooops, sorry on the length of delta. Should read √(15,706,954.24034) - 3963.2 miles.
"We have reason to be thankful for fools. It is quite wonderful … to see how large a share stupidity and unpractical conservation and dogged superstition have had in preserving for us traces of the history of our race, which practical utilitarianism would have swept away." (Primitive Culture p. 14, E.B. Tylor)
If you believe there is significant light refraction far more than the curvature of earth, so images we see 40 miles away are just the bending of light, maybe we can conclude we live on a flat earth because of the bending of light. Even it is was curved, we cannot perceive it according to refractearthers.
I still havent received a satisfactory answer from anyone to the question "how big does a body of water have to be be before the surface has measurable curve?" i have done this on a small lake with a laser level accurate to 1000'.
I have asked surveyors at a lake that is 4 miles long they said it is exactly the same elevation at both ends of the lake. So if its not 4 miles perhaps 10, 20, 40? I dont have the capability to shoot those distances personally but i'm sure someone does and could answer this question for me. Somewhere between 4 miles across and the ocean( which obviously has to curve) there is a point where it goes from perfectly flat to curved. What is that point?
The point where you go from flat to curved is dictated by your ability to measure accurately, not the liquid. The surface of a liquid on Earth is always curved. For small enough distances, we can ignore the curvature. In the case of short distances, wind and waves may make accurate curvature measurements impractical. However, there is always a curve.
Did you just say "the liquid in the surface of earth (a sphere) is always curved"?
Can a fucktard flat-earther please help de-brainwash this poor fellow. He might try and say "gravity". Oh boy....
So you say. Well, I’m a globe believer now! Gee thanks!!!
You actually said that the surface of a liquid on earth is always curved? Please give your sources for that claim.
The bulge in 1000ft is only 7/100ths of an inch. Meaning that if you took a laser and set it at six feet on one side of a 1000ft lake and adjusted it so that on the other side, the laser was at six feet. At midpoint the distance to the water from the laser would only be 6 ft less 7/100ths of an inch.
Too insignificant to accurately measure.
Kevin McMillen
Are you saying that the surveyors equipment isnt accurate dead level but actually measures curve? They said two ends of 4 mile lake are perfectly level
The lake is perfectly level within the accuracy constraints of your instruments.
That's horse poop pardner
Tater — Horse poop is a good substance in a substrate to grow potent psychedelic mushrooms. Of course, there are other constraints to be considered, as within any process. But that's mathematics. … … and maybe a smidge of materialism — shazaam!
what is level? Is it an equal distance from the center of earth?
It depends on the level of accuracy you are looking for. If we assume the Earth has a uniform gravitational potential, level means equal distance from the center of the Earth. For EXTREME accuracy, you would need to include the non-uniformity of gravity – Earth's gravity is lumpy. The surface of a liquid then would be described by an equipotential surface.
Earth’s gravity is what? Lumpy? OMG Where did you find that gem? I can’t stop laughing, wow.
David Musser, you must be laughing at yourself. "The truth is out there" Lumpy is a good metaphor for earth's gravity. You do understand metaphor, don't you?
In geodisy there’s a “significant” difference between where a plumb bob points (gravity) versus the “center” of the earth, depending on where you are on the planet, based on varying earth densities. GPS technology has been relying on accurate calculations of the geoid (the lumpy effect of the gravity model) vs the spheroid (the purely perfect mathematical model of our earth, slightly out of spherical). So yes, the gravitational shape of the earth as a mathematical model is lumpy and is relied on for measuring large navigational distances and is why I can have 1/8” datum accuracy horizontally and 1/4” accuracy vertically anywhere on the planet with my 25 year old GPS system. For you flat earth lurkers out here, explain to any surveyor how now 29 years after Clinton made the the already 30 year old GPS system public domain, all the giant GPS service providers (Gaarmin, TomTom, NavStar, etc) are apparently colluding not only in the US but with several large international GPS satellite systems (Japan, Russia and China) to lie to the world about their reliance on the fact that were on a spinning globe spiraling through the cosmos around our star. If you have even the simplest understanding of GPS it’s impossible to believe our earth is flat. Side note - the authors explanation of refraction as Caracas visibility goes is fascinating, makes sense and explains why I can see almost all of Kaho’olawe from the shores of north Kona, Big Island.
The way i understand it surveyors equipment is run by gps coordinates therefore one part is elevation so if they took a grade shot at the end of a 50 mile lake on a calm day and then shot the other end and it was exactly the same i dont see how we could deduce that the earth is round.It would seem to me to be more like a many sided polygon of some sort. If i look at any picture that they claim is earth from space they appear to be almost perfectly spherical
Have you considered the effect of the atmosphere on images from space? Have you considered the human proclivity to misinterpret its sentient inputs? Have you considered illusions? "Hallucinations are are a fact not an error; what is erroneous is a judgment based up0n it," Bertrand Russell. Of course, there is always human denial to ignore — human psychology, study of the metaphysical expression of the non-material adaptations of biological matter, the bipedal tube. What is truly amazing are the claims of intelligence made by bipedal tubes.
A lot of leveling instruments actually use water or other liquid to find level. So if gps isnt accurate enough to detect any measurable curve in the surface of water( the substance used to determine level on earth) then why immediately jump to the conclusion that its curved but we just cant measure it. If the surface is curved it has to be measurable at some point. if we cant measure the curve i would then say it must be flat. Although it might be equipotential also as i do not know what that means
Using water for level is a very good way to obtain a practically level surface. I am not saying it is not measurable -- its curvature matches that of the Earth, which we can measure. For short distances, it is not worth measuring or not practical because of wind, waves, or whatever.
As for equipotential surface, check out the Wikipedia.
You say the earth’s curve is measurable. Would you please publish the measurements which you have taken and the coordinates or landmarks you used? Thanks
Lake mead when full is 120 miles long. Its elevation is 1229' above sea level at both ends.
Earth is approx 24000 miles circumference. Lake mead length represents about 1/2% of the entire distance around and there is no measurable curve
Who told you there is no curve? It curves just like the ocean.
So there is no such thing as level to you. Just varying degrees of curve. If you plotted a perfectly flat plane in a total station and marked those points on a calm lake they would all touch the surface of the water. A total station does not have any thing built in to account for any curve of the earth. If you built two mile high buildings perfectly plumb a mile apart would the distance be farther at the top?
When i see chicago from michigan city all the buildings go straight up rather than diverging from one another
I view level as a useful idealization. To some degree, everything is curved by gravity – even space itself.
You are asking excellent questions! It is absolutely true that two structures built plumb and one mile apart actually diverge. In fact, this effect must be taken into account for some designs (e.g. Verrazono-Narrows Bridge). I will quote from the Wikipedia.
You cannot see the buildings diverge from each other because the curvature displacement is on the order of inches. Only in precision construction, like suspension bridges, must it be taken into account.
If the earth is flat and the buildings in Chicago are so apparently visible from a particular vantage point, then Mt. Everest, which is the tallest mountain in the world and in the northern hemisphere, must also be visible from that same location. Ok, so maybe you need 30x or greater binoculars, but it and other Himalayan peaks should be visible, as also, many peaks of the Andes (albeit in the southern hemisphere) and Denali in Alaska and Whitney in California (both in the northern hemisphere) from that vantage point.
"Lake mead when full is 120 miles long … Earth is approx 24000 miles circumference. Lake mead length represents about 1/2% of the entire distance around and there is no measurable curve."
24000 miles x .5% = 120 miles
.5% of 360˚ = .0075˚. .0075˚ x ∏ = .02356 radians. Any portion of a radian greater than 0 (the point which is the radian of 0˚) [nice gerund here] is certainly a measured curve. That one may not perceive it is as a curve is a sensate misperception, not an error of measurement.
"Think of how stupid the average person is, and then realize that half of them are stupider than that," George Carlin.
Hell, I’m in the top 5% regarding tested intelligence, and I, as a generalist, have realized that I’m pretty damned stupid. So I think of those "smarter" than me. They are specialists in stupid.
Rules of perspective null that point. A kid on the near-side beach of Lake Michigan will appear taller than the Chicago skyline 50 miles across the lake. Everest, 7606 miles behind those towers would reduce due to perspective down to the height of less than the curb height in front of the Willis Tower. In short, it would be completely impossible to see, due to size and all the stuff blocking it between Chicago and Nepal.
When the weather channel says visibility is infinite, then yes, you would be able to see all those mountains from one vantage point. We are limited only by our perception, eye sight, and visibility. There is no measurable curve, anywhere.
George Carlin was talking about you when he made that statement... Take a 3d drawling class and learn vanishing point perspective... Also isn't it obvious they came up with the circumference from equating it with the hours in a day? Why is it that every explorer in the arctic lower hemisphere always documents wrong calculations... Earth is a magnet and all matter and organic and inorganic life are electric in nature... The van allen belts are the firmirment which is a toroidal magnetic field... Gravity is nothing more then magnetism, the false physics that the masses are told among a bunch of other falsehoods are meant to confuse us to what the nature of reality is so we can be more easily controlled... Once you realize this you will understand that there is a working unified field theory based off of occult aether electromagnetic science which allows for all the paranormal and sci-fi technology to be taken seriously... We all emit our own electromagnetic field and so does all organic life which is why so many animal in the ocean and birds in the sky are dying off because of the disturbance of the earths natural system of frequencies they rely on for communication and navigation... I don't know if the earth is flat or a sphere but there is enough evidence if you allow your self to take it in that it is flat and the sun isn't bigger or farther away... Notice how all the alien stories are being connected to historical a biblical events and stories? Better yet what about all the theories and scientific organizations responsible for "space" which are associated with occult magic, nazis, mind control, secret societies, hollywood/disney and science fiction writing... It becomes obvious why the world is so fucked up and who is responsible and how and why its done when you realize that this equation (8" of curve per mile) squared shows the earth isn't a sphere... I suggest you go look at the origins of nasa along with well documented bloopers and throughly research the fantastical claims of Tesla who's technology is still being slowly released to the public even today as well as nasa extensive high altitude balloon system before you can say for certain that the earth is a sphere. Maybe read the Luciferian Doctorian, look up Young Blood treatment, Pope Innocent the 8th and pedogate..Warner Von Braun had a passage from psalms on his gravestone about the firmament and warned of a fake alien invasion... Its not easy for someone to say that the earth is flat because it goes against everything they were taught and its extremely unpopular, yet people who do usually have been avid nasa and space/science enthusiasts there whole life.
so in other words, the curvature of the earth plane is merely a hypothetical construct, which has never been backed up, never been proven by any actual real measurement of any actual real curve, The laser experiments were inconclusive due to the methods and equipment used, and the ones allegedly conducted by Mr. steven hawking were particularly sloppy theatrical events which didn't actually measure anything apart from peoples' gullibility.
According to the formula to calculate the horizon distance that you could see, If you are about six feet in height you should only see about three miles.
https://dizzib.github.io/earth/curve-calc/?d0=30&h0=100&unit=imperial
If you are on the bank of a river and the other side is six miles and you could see the land then the earth is not that round as they say it is, check this out for yourself.
hi...1.169 times the square root of the height of a given object determines how far it can "see" the horizon.
Take your example... 6 mile wide river. 6 foot tall john looks across and sees the other side.
1.169 times square root of 6 feet equals 2.863 miles that he can see if the horizon is unbroken by objects.
Now, what Tall John sees across the river is not the rivers edge where it meets the land. He is objects that are tall enough to exceed the 2.863 mile limitation his height of eye has.
Examples of how it works.
1: Tall John is looking across the river for Tall Jenny. Jenny is also 6 feet tall.
John can only see 2.863 miles and Tall Jenny because she is 6 feet can also only see 2.863 miles. Add their range of vision together and you get 5.726 miles leaving a gap of .27 miles in the middle that prevents each from seeing the other.
If Tall Jenny climbs up a 4 foot embankment she increases eye height to 10 feet which gives her a range of vision out to 3.69 miles.
Combine her new range of vision to Johns range of vision and the can see each other. 3.69+2.863= 6.5 miles.
They can only see each others eves at this point. the higher they get, the more of each others bodies they will see.
SO a tree that is 100 feet tall on the other side of the 6 mile river can be seen by john easily because it is much higher than the he minimum height need to be seen by John.
the tippy top of that tree can see for a distance of 11.6miles. John will see the upper 3/4 of the tree from his vantage point.
Does that help?
Regarding the river six miles wide (Godfrey C. Archer), I recommend Alfred R. Wallace and The Bedford Level experiment which was about 6 miles and curvature.
All these calculations are neat and all, but can anyone prove that the earth actually has curvature ?
Have you ever looked at the Bedford experiment?
mark
I have looked, at six miles, curvature would result in the row boat, and the man sitting in the row boat to be completely beyond the curvature. Which, of course was proved false. We do not live on a ball.
Hey Doug, lighten up.
Consider Matt’s statement about railroad tracks which he conflates to air planes and sea level, "Railroads are built level. You say you couldn’t use the same benchmark to build hundreds of miles of track yet every airplane on earth uses “sea level” as the reference point for their altitude." This conflation is the result of Matt’s two dimensional logic.
Perhaps offer a challenge to Matt from his two dimensional perspective. For example, ignoring the false assertion, "railroads are built level" (perhaps Matt is a shut-in who has never seen a rail-line on a mountain), it is evident when one on a prairie looks down a line of RR tracks while standing between them, one observes very clearly that they obviously meet in the distance, railroad travel beyond that point of joining of the two tracks must be impossible. So the flat-earthers must have a way of explaining how freight can be carried coast to coast by trains.
An alternate 2D challenge to that is when a train passes the observer who then stands between the two tracks and watches the train move away down the tracks that consistently close upon themselves, the train is quite obviously seen to get smaller and smaller. The flat-earthers must explain what keeps any persons on that train from compression injury.
One more alternate 2D challenge; when one stands at sea level on Ocean Beach in San Francisco, CA, why can they not see Mauna Loa, a Hawaiian mountain greater than 13,500 ft (4100m) in altitude, or the even greater altitude of Mt. Everest over 5mi. (880k) in the Asian Himalayas. It is the case that on a fogless day while standing on Ocean Beach, one may see the higher altitudes of the Farrallon Islands, the greatest elevation being less than 350ft (106m) above sea level, or the more distant but lower, less than 330ft (100m), Point Reyes peninsula.
Like all flat-earthers, Matt needs empathy and guidance, not a rude ad hominem. Find ways that express your gratitude that you are not stuck in the two dimensional logic of flat-earthers. Question Matt in regards to his two dimensional logic, such that he must provide answers so others may 'see' more clearly his two dimensionality.
Have you ever taken into account the curvature of earth in any aspect of your life? If the answer is no then you are also a flat earther. Until you actually have to adjust or compensate for curve or spin you are operating day to day as if it is flat and stationary. I do appreciate comments that don't just call me stupid. Although you kind of did in a round about way. Thanks for your feedback.
One word. Visibility. If visibility where infinite, then yes, you would be able to see from one side of earth to the other.
Funny, I can see the moon, and the moon is farther away than 6 miles. Yes visibility is infinite. Even on a false flat earth model the moon is still farther away than 6 miles, yet I can still see the moon. Maybe curvature has something to do with visibility?
Matt, you asked, "Have you ever taken into account the curvature of earth in any aspect of your life?"
Obviously I have taken earth curvature into account in at least one aspect of my life since I am contributing to this conversation. So sorry your two dimensional thinking does not make that obvious to you.
Sad.
No compensation is required of me to personally adapt to the curvature of the earth or to its spin. Now if the earth were to stop spinning …
Oh, forget it, the "…" suggests a creative imagination which is beyond that of the two dimensions of your logic.
Sarcasm I like. Condescension, not so much. Thanks for your consideration.
What are the assumptions of methodologies for calculating curve and straight surfaces
mathscinotes, Thank you for your original post. I am a generalist, not a maths person. I never took calculus. I had to break out my old HP 11C and do a lot of refreshing of understanding to arrive at the following. It has taken me over several days to achieve. While I may not have arrived at an accurate result, I understand I’m damned close to nothing. Mental exercise is good and part of my daily routine. So even if I’m wrong, I’ve had a lot of fun.
Using your figures of the earth radius in miles and a horizontal line 100 of feet, I converted the radius to feet, 20,925,696 ft. Since tan = opposite over adjacent, the angle from the center of the earth can be ascertained.
100 ft/20,926,696 ft = .000004784 ft which is also the tan of the central angle.
My HP 11C gave me
arctan .000004784 = .000027410˚ = central angle (a smidge under 1˚)
and it gave me
.000027410˚ = .000000478 radians (the ratio of the described arc to the circumference of the earth’s circumference expressed in feet)
The point is, if my perceptions and calculations are correct, then when expressed rounded to 5 digits, the tan and radians are not separable, or, this as an instance when 100 feet is not even a prick.
You are correct that the tan(θ) and θ are very nearly the same for small θ. Same with sin(θ) and θ for small θ. I commonly use this approximation myself. If you want more details on these approximations, see this Wikipedia article.
mark
Thanks for the Wiki article. I will spend some time with it. I'm slow and old. But I do have a fast RPN calculator. 😀
My question concerns the conceptual model being used, not the mathematics. Using the Pythagorean theorem and the right triangle formed by the center of the Earth, the observer's eye, and a tangential line of sight from that eye seems misleading to me because I can angle my view downward to see something that is far away. This changes the shape of the triangle, breaking the simple application of Pythagoras. I tried a similar calculation (using this web site to speed things up: http://www.handymath.com/cgi-bin/arc18.cgi) in order to find the sagitta, or height of arc above the chord, given a known distance between the observer and target, or arc length. Assuming that the referenced calculator is accurate, and that I used the correct numbers for the radius and length of arc, this gives me a value of barely more than 2" for a target that is 1 mile distant with the viewer at sea level, 8" over 2 miles, and 18" over three miles ((miles squared) times 2 inches). Ignoring refraction, waves (or hills), and other irregularities, this suggests that I should be able to see to within 2" of the ground at one mile, instead of the 8" that your method (also used by many others) gives. Since that number represents the "height of the hill" between the observer and the target, why is the sagitta not used to compute line-of-sight loss due to the curvature? What am I missing?
You're missing the fact that you are standing above the surface of the earth, not lying down with your eye on the ground. If you are 6ft above the surface, then you are looking 'down' at the horizon. When your line of sight 'grazes' the surface, that is the tangential line.
That is not how I interpret the diagram on this page (and others). From the image and the accompanying description ("Analysis" section, above), we are solving for δ, which is the drop over the indicated distance. R is the radius and indicates the location, and presumably includes the height, of the observer. The tangent in this diagram touches the Earth at the point where the observer is standing, not at the point at which the observer's line of sight touches the curve. The solution shows how much the curvature of the Earth deviates from the horizontal ("x" in the diagram) away from that point, but does not appear to account for the change in angle of observation. Again; I have no argument with the Maths, I just think that the equation is solving for a value that is irrelevant to the real situation. Maybe a different/better diagram would help me to see how I am mistaken?
R is the radius of the earth, delta is the height of the observer's eye (or measuring device) above the surface. This same delta could also be looked at as the drop from horizontal (tangent line) if your eye (device) was at ground level at the tangent point. It's just a matter of whether you are using a known delta to solve for distance or a known distance to solve for delta. Regardless, the math is sound, but the entire situation is idealized and unrealistic. One would be hard put to measure the earth's curvature over any short distance because the errors inherent in the instruments and their references to level swamp out the measurement itself. For example, you have a visible laser and set it up 'level' to aim at a distant point and note that the 'spot' is 6 in below the height of the laser at the other end. Is the earth curving up? No, your laser just wasn't as 'level' as you thought.
I'm trying to understand why in figure 1, you use the entire radius (R) of the earth (as everybody else does too). However, from a point of height h above earth's surface, the effective visible distance (Dh) to the horizon (for geometry only, ignoring refraction etc.) is much less, it being Dh = sqrt(2hR + h^2). So with respect to an axis of the earth (carrying our observer), the radius of visible curvature should be r = Dh*R/(R+h) ~ Dh (if h much less than R), which is of course way less than R. Therefore, the perceived curvature of the earth from a height h should be much more than what you present.
Bedabrata Pain, try placing the center of your viewing lens on the ground immediately above the point of tangency of the earth with the radius, say at most an 1 inch, depending on your choice of lens. This in relation to a radius of 20,926,696 ft. You may get a more satisfactory understanding.
Pingback: Earth’s Curvature and Battleship Gunnery | Math Encounters Blog
I could not verify your equation when I checked it using x as the radius of the earth.
But when I plug in the known given deviation of 8” per mile I do get close to your number. But it is off by a decimal place or two.
0.000126262626263
Oops. I forgot to add the 100 feet. So I would need to multiply
0.0001263 by 12 then 100 =0.151515151515152“ per 100 feet. Check .151515 x 52.80=8”.
But this answer I gave is incorrect too. It is a radian equation since there are circles involved. The closer to the beginning of the arc the less deviation. The furthest away from the beginning is the greatest. And is limited to the radius.
Hi Chuck,
I am not exactly sure what you are trying to compute, but let's assume that you want to show that the Earth curves 8 inches over a mile of horizontal distance. The calculations go as follows.

Because I use Mathcad, units are handled automatically. This may be confusing for some. I have tried keep the units simple in my example here. I am guessing that you have a units problem.
mark
The only thing necessary for triumph of evil is for good men to lay waste convincing others "Earth is flat".
I've read, seen, researched and verified all "evidence" I could find and I'm still not convinced the Earth is flat, sorry. And now for something completely different...
https://flatearthinsanity.blogspot.com/2017/06/where-is-curve.html
Hi, can update website to include picture and number, so they can see the number on picture, and explain why need to divide and multiply, and explain each thing that you have to use and why you use that. So, it is simple as 1 + 1, that is you can see 1 represent 1 that is separate from another 1, and + is to add together to equal 2. So, I understand R, that is earth, so it is R plus target distance, so the Combine of Radius is higher radius, and above tangent line, so R is tangent line, so need to wide apart from horizontal that you are seeing to tangent line of earth which it is lower radius in distance. It is triangle as it is three number that is center point to surface point of earth that is radius, so the gap point, and another radius is explain above. And I can see ya use three number which represent triangle, but you convert to more than 3 number to get answer, right? Well, three numbers, plus symbols, I understand if use simple symbols that is add, subtract, divide, multiply, so you use square root so that is opposite of ten to power, right. Why not ya make it simple and use only four easy symbols, ya have to use square root? And explain the represent of using square root, and power of tens, etc. Well, add, subtract, etc is easy to understand. And between two top vertical that is a gap of horizontal line, so why ya use that formula and why R2, etc?? It is because it is 3d, that is horizontal radius on horizontal plane and horizontal radius on vertical plane, so it becomes a curve on earth that is 1/ something on earth. So, it is same as 3.14 divide something to equal that curve of arc diameter. The diameter of thru globe earth that is longest is 7926, so it becomes an arc that is 24887.64, so 3.14 bulge out the diameter of 7926 to 24887.64. So, it is 24887.64 all over the earth, since 3.14 is all over as represent diameter that divide circumference. So, the above it is accurate that the radius as a curve that is an angle, so it is an angle plus gap size that is missing, which it is the gap size of certain number to add to radius of 3963.2, so it would be accurate, so it comes down radius must be same all over, so it is 7.994 inchs that is 100 feet from tangent line plus horizontal line of 90 degree from your head. So, it would be good to have check up math like 1 + 1 is 2, so 2 - 1 is 1, so it is simple as you can see, so it balance out of two. So, I see you subtract R which I understand to means to remove that radius because that radius is connect to target distance, so you want to focus target distance on the earth, not inside the earth, so the target gap distance to radius is 7.994 inches. So, there two counter math that can check 1 + 1 is 2, 2 - 1 is 1, so to two math of opposite size, so there is opposite side of triangle which you can check to be accurate. Calculate is not enough since it may be accurate but can be understood? It is best to understand then use calculate so you know calculate is accurate and not misleading. Which the people can mislead you which you know about flat earth, that doesn't means flat earth is misleading you but globe earth is misleading you.
Considering the flatearther aspect, the better advice might be to take a flat plane, a noon start spinning it …
Thank you for affirming that man is gullible and self-deceiving.
I have been trying to understand the relationship gravity has to the curve of the earth. Imagine you have a perfectly flat disk that has a radius of 5 miles. The center of the disk is perfectly level and touching the ground. The edges would be approximately 16 ft off the ground if the ground were relatively smooth throughout the area of the disk. What would happen if water were to be poured onto the disk until it spilled off the sides? How deep would the water be at the center of the flat disk? Since water is self leveling it would be 16 feet deep at the center, correct?
I would point out that ocean going ships are limited to ~1,250' in length due the prow and stern of the ship begin to rise above sea level and impose undue stress on the hull.
Very interesting. but i think lots are a little to buoyant. get to caught up in science. Like the balloon in the ocean. Some explain down coming to center of the earth, no matter where you are at on earth. they say down is towards the center. Here is a question for that: since we all know the masonic order of things. lots of trickery in yalls math. That big machine that digs all these tunnels under the earth. I want one of you math wizards to get in it. Start on north pole. Figure your wizard math for a straight line to south pole. Ok, you are going DOWN. As you get to center and pass that point.. A magic trick flips you then you drilling up to go out the other side to south pole.. if anyone with all this buoyancy (hot air) believes the lies. Their math is wrong. off by 9 What is 9? 9 is same crap yall believe from above post.
if it was a constant 8 inches every mile it would be a downward slope not curve like sphere. I believe the calculation becomes exponential after first mile.
Chad is correct, 8 inches per mile squared results in a parabola. Only the very top of it could align with a small (very small) part of a sphere. Making that calculation only good for a few miles.
Then you need to do some long distance shooting, cause their is absolutely no such math added in for curvature lol you are foolish at best.
Do a little more research bud.... and of course they don't want me to respond with this cause too many people said it lol. By the way, why does this site not allow you to vote on certain comments lol they stop you from disagreeing with the writer
Long distance shooting already takes curvature, drag and gravitational forces into account. These and other factors are absorbed into the bullet drop over distance which is measured empirically at certain points, not calculated. The calculation is to fill in the curve from the points (interpolation) and adjust for wind speed and direction.
I have done miles and miles of pipeline and road and never adjusted for the curvature of the earth. I have been in the Civil Engineering field for over 40 years!
There is only one elevation system. The system we have says: 1,000 foot elevation is 1,000 foot elevation at a level plain 100 miles away. So, we are applying a level elevation system to a ball. How exactly does that work? At 100 miles away, elevation 1,000 is elevation 7,667 on a level.
Unless we use the center of the earth as a reference for all elevations, our current system does not make any sense at all.
What do I know? I am just a mathematic major at Cal Poly and deal with survey and elevations for the past 40 years.
BTW I just became awake!