Nuclear Battery Math

Quote of the Day

In any project, the important factor is your belief. Without belief, there can be no successful outcome.

— William James

Introduction

My sons always tease me about my interest in space. In order to understand my interest in space, you need to understand what it was like being a boy during the 1960s. I had my own October Sky boyhood. I built rockets, read everything I could about space, built electronic circuits, and dreamt of someday being an engineer and space traveler. While the space traveler part didn't work out, I was fortunate in that I did everything else that I dreamt about it. I have met numerous engineers who are now in their 50s who had the same experiences.

I still read everything I can find about space. Recently, I was reading about Mars Science Laboratory (MSL) and noticed that it has a Radioisotope Thermoelectric Generator (RTG) for a power source. Figure 1 shows an artist's rendering of the MSL with two RTGs, which NASA refers to as the Radioisotope Power System (RPS).

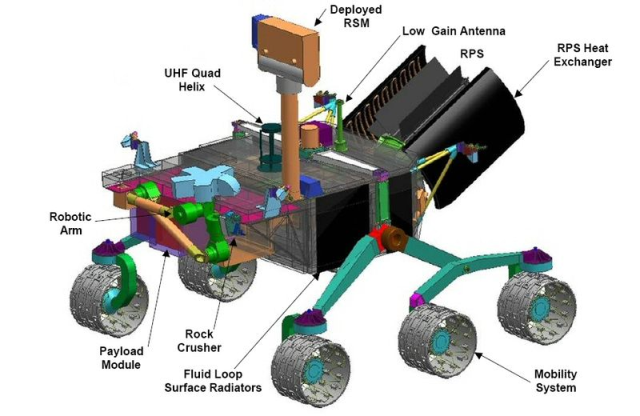
Figure 1: Mars Science Laboratory Rover with Radioisotope Power System (aka RTG-based Power System).

MSL's use of an RTG got me thinking about a physicist I sat next to on a flight years ago. He worked for Medtronic and had assisted in the development of a "nuclear battery" for use in a pacemaker. It was on that flight that I learned a little bit about RTGs. Let's see if we can use a bit of math to understand how an RTG works and how it is used on the MSL mission. As usual, I will be using Mathcad for the heavy lifting.

Background

Referencing the Wikipedia, lets start with a definition of what an RTG is:

A radioisotope thermoelectric generator (RTG, RITEG) is an electrical generator that obtains its power from radioactive decay. In such a device, the heat released by the decay of a suitable radioactive material is converted into electricity by the Seebeck effect using an array of thermocouples.

Figure 1 (Source) shows a photograph of the RTG used on MSL, which is called the Multi-Mission RTG (MMRTG).

Figure 1: Photograph of MSL's MMRTG.

I saw the following statement in The Atlantic Magazine about the MMRTG:

The 43kg MMRTG is designed to produce 125 watts of electrical power at the start of the mission, falling to about 100W after 14 years. (NASA/Kim Shiflett)

Let's see if we can use this one statement to derive some information about the MSL's RTG.

Analysis

Amount of Power Required

A thermoelectric generator requires heat to produce electricity. Unfortunately, thermoelectric generators are notoriously inefficient. NASA has reported that their efficiency level is about 6.2%. This means that for every 1000 W put in, only ~62 W of electricity comes out. Since this generator is specified to put out 125 W, we need a heat source that produces . The Wikipedia entry for the MMRTG states that it dissipates 2 kW of power, so we appear to have the correct total power figure and efficiency.

Heat Generated by Radioactive Decay

When a plutonium-238 atom decays, it emits an alpha particle with a decay energy of 5.593 Million Electron Volts (MEV). It is this decay energy is the source of heat (i.e. energy) that will be converted to electricity by thermocouples. This heat is enough to cause the Pu-238 to glow (see Figure 2, Source).

Figure 2: A Glowing Pu-238 RTG Element.

Radioactive decay versus time is usually modeled mathematically using the concept of half-life. Equation 1 shows how half-life is used to model decay.

Eq. 1

where

• t is time in years.
• t_HL is the half life of Pu-238 (87.74 years).
• N is the number of atoms in a sample of radioactive material.
• N₀ is the number of atoms in a sample of radioactive material at t=0.

To compute the power radiated by a sample of Pu-238, we need to determine the number of decays that occur per second. We can compute the number of decays per second by differentiating Equation 1, which I show in Equation 2.

Eq. 2

Let's say we want to compute the amount of heat generated by a gram of Pu-238. We need to determine the number of Pu-238 atoms in a one gram sample and apply Equation 2, which tells us that Pu-238 generates 0.568 W/gm of heat. Figure 4 illustrates this calculation. We can use this number to estimate the amount of Pu-238 that we will need to generate 2 kW of thermal power.

Figure 4: Calculation of Heat Generated Per gm of Pu-238.

Amount of Pu-238 Required

Since we know that we require 2 kW of thermal power and that Pu-238 generates 0.568 W/gm, we see that we need . This agrees with the value 3.5 kg stated in this presentation from the Department of Energy, so I think we understand how much Pu-238 is required.

Degradation of Performance Over Time

The quote from The Atlantic Magazine states that the electrical power available from the MMRTG drops to 100 W after 14 years. Let's assume that we have a fixed percentage of degradation year over year, which is similar to a compound interest problem. We can determine the percentage decline per year as shown in Equation 3.

Eq. 3

So the output power is declining by 1.58% every year.

The amount of heat available from a radioactive source degrades every year because the amount of radioactive material reduces every year because of decay. We can compute this decline in thermal power as shown in Equation 4.

Eq. 4

So thermal power declines by 0.79% every year, which is about half of the electrical power drop reported by NASA. However, the thermocouples also degrade in performance every year. So the 1.58% degradation rate is composed of two parts: (1) the reduction in available thermal power due to radioactive decay, and (2) the reduction in thermocouple conversion efficiency over time.

It turns out that there is data from Voyager on RTG power reduction. Over a 33 year period, Voyager has seen its available electrical power decline to 67% of its initial value, though its available thermal power has only declined by 83.4%. This means that Voyager has seen a decline in electrical power generation of 1.7% per year while its thermal power has degraded by 0.79% per year. So that 1.6% degradation expected for the MMRTG by NASA seems reasonable.

Conclusion

I was able to calculate some important characteristics of NASA's power system for the Mars Science Laboratory. I could see problems like this being good ones for calculus students to sharpen their skills on.

There are folks looking at how to improve the efficiency of nuclear batteries (example).

Save