Introduction
A reader asked a question that I answered in a comment response, but others may be interested so I will include my response as a post. One of my most read blog posts is about the amount of vertical deviation that exists between a level line and the Earth's surface. A reader of that post asked a related question. She measures the distance to sea life from an observation point on a cliff and was wondering how to compute the difference in distance between the arc length and the horizontal distance to an object on the water. This is a nice exercise in geometry.
Background
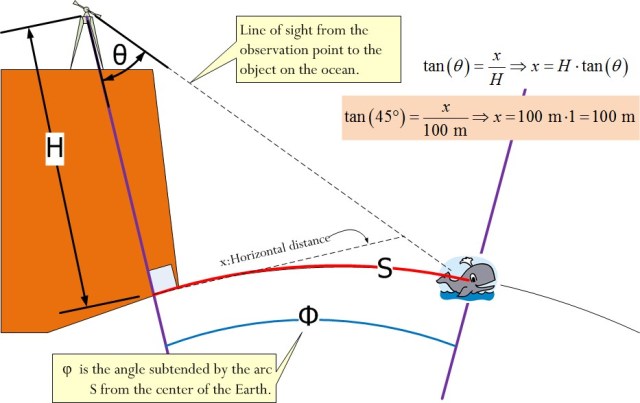
Figure 1 illustrates the measurement scenario. H represents the height of her observation site above the ocean. θ represents the angle measured by her theodolite.
Figure 1: Observation Scenario for Sea Life.
Figure 2 illustrates the basic geometrical aspects of the problem. R represents the radius of the Earth. D represents the distance to the object.
Figure 2: Basic Geometry of the Observation Problem.
Analysis
Figure 3 illustrates my analysis. The question posed wanted me to assume a cliff height H = ~100 meters and an observation angle θ = 45°.
Figure 3: Analysis of the Observation Problem.
The horizontal distance to the object is 100 meters and the arc length to the object is 100.00076 meters. This is a very small difference.
Conclusion
The amount of distance error introduced by the curvature of the Earth for short distances is very small and would be difficult to measure. However, the error could be significant for long distance measurements.
Pingback: Straight, Level, and the Curvature of the Earth | Math Encounters Blog
I like the way you combine math and logic. Help me out here. I have recently stumbled on some proofs for the Earth's being flat. Seems bizarre. Some of the proofs are related to this curvature thing. You make the point that in small distances the curve is negligible but as we square "x" at greater distances, it is something to contend with. An engineer laying railway over a 1000 mile distance would have to contend with 128 miles of curvature and yet they are said to have laid tracks with no regard to the Earth's curve whatsoever. Is my math right? Could this be? Help.
John Hill
John hill why exactly are thhe engineers having to "contend" with the curve? This appears to be something of a straw man argument to me. Esp lnowing flat earthers.