The pessimist complains about the wind; the optimist expects it to change; the realist adjusts the sails.
Introduction
Figure 1: Tall Ship Europa Under Full Sail.
I have lived most of my life in Minnesota, which is about as far away from the oceans as you can be in the United States. The idea of a planet mainly covered with water has always fascinated me. I will never forget the first time I saw an ocean (Pacific, Santa Monica, CA 1982). Fortunately, my work has provided me a bit of experience on ships and that experience was career changing − my early ocean experience involved laying fiber optic cable and that set the course of the rest of my career.
Today, I satisfy my nautical longings by reading about celestial navigation and the age of sail (e.g. Figure 1). I have been reading a book called "The Lo-Tech Navigator" by Tony Crowley and it contains a number of low-tech, navigation-related projects that I want to build. While reading the book, I ran into a rule of thumb that I thought I could derive here using a bit of vector algebra. The rule of thumb tells you the course correction (in degrees) required to compensate for the cross-current. I would state the rule-of-thumb as:
A 6° course correction in the direction from which the current flows is required per 10% of cross-current velocity relative to the ship's velocity.
To illustrate the rule, consider a ship sailing at 10 knots with a cross current of 1 knot, which means the cross-current velocity is 10% of the ship's velocity. The rule-of-thumb states the skipper must adjust his course by 6° in the direction from which the current flows to compensate for its influence.
My goal here is derive this rule of thumb. Let's dig in ...
Background
"The Lo-Tech Navigator" contains Table 1, which presents both the required and rule-of-thumb course correction for a small set of cross-currents. I want to duplicate this table.
| Cross-Current Rate (knots) | Correction to Main Course (°) | 6° Rule of Thumb |
| 1 | 5.7° | 6° |
| 2 | 11.5° | 12° |
| 3 | 17.5° | 18° |
| 4 | 23.6° | 24° |
| 5 | 30° | 30° |
| 6 | 36.5° | 36° |
Analysis
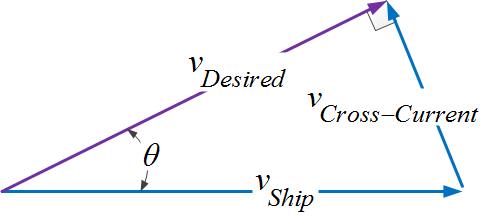
Figure 2 shows the velocity triangle that represents the motion of a ship relative to the water and Earth.
Figure 2: Vector Model Of Ship Velocity in Cross-Current.
Equation 1 shows the formula for the course correction, which assumes that the current is perpendicular to the desired direction of travel. Of course, this would rarely be true in practice, but the book goes into corrections to the rule-of-thumb to deal with currents that are not perpendicular to the desired direction of travel. I will not deal with these corrections in this post.
| Eq. 1 |  |
where
- vDesired is the velocity of the ship in the desired direction.
- vCross-Current is the current velocity, which is assumed to be perpendicular to the ship's desired course.
- vShip is the velocity of the ship relative to the water
- θ is the angle deviation from the ship's desired direction required to compensate for the cross-current.
Figure 3 shows a screenshot of my Excel worksheet that tabulates Equation 1. The result is identical to the table in "The Lo-Tech Navigator".
Figure 3: Screenshot of My Excel Version of Cross-Current Correction.
Conclusion
The 6° correction per 10% of cross-current relative to ship's velocity is a useful rule-of-thumb. It also is a nice illustration of the use of vectors in what was an everyday application during the days of sail.