Quote of the Day
Present to inform, not to impress; if you inform, you will impress.
— Fred Brooks
Introduction
I have a boring task that requires that I be able to access a geographic database to gather a large amount of information. There are numerous databases out there, but the Wikipedia Geonames database is the one I would really like to learn how to use – it is large and free. I am not particularly skilled at web scraping and I have been procrastinating on my task for a while. I need a interesting problem to drive my interest.
Yesterday, I was reading about Mt. Everest on the Wikipedia when I saw the following statement that aroused my curiosity about the shape of the Earth.
The summit of Chimborazo in Ecuador is 2,168 m (7,113 ft) farther from Earth's centre (6,384.4 km (3,967.1 mi)) than that of Everest (6,382.3 km (3,965.8 mi)), because Earth bulges at the Equator.[6] This is despite Chimborazo having a peak 6,268 m (20,564.3 ft) above sea level versus Mount Everest's 8,848 m (29,028.9 ft).
Mount Chimborazo is shown in Figure 1. While I have never heard of this mountain before, it apparently has the distinction of having a summit that is as far from the center of the Earth as a point on land gets.
I can see a little math here and now I start to stir. What if I constructed a list of the mountain peaks furthest from the center of the Earth? That would give me a problem that I am interested in that would also allow me to learn how to use the Geonames database.
Let's dig in ...
Background
Objective
My goal is generate a table of mountain heights sorted from by distance from the center of the Earth. While accomplishing my goal, I will also:
- learn how to grab data from the Geonames database.
- learn a bit about geodesy – the study of the shape and gravitational field of the Earth.
All of my work today will be done in Excel and I will provide a link to my spreadsheet at the end of this post. There will be a small Visual Basic for Applications (VBA) program used with Excel to access the data.
Definitions
A big part of this effort is getting all the terms defined. Here are the definitions that I used.
- Reference Ellipsoid
- In geodesy, a reference ellipsoid is a mathematically defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body. Because of their relative simplicity, reference ellipsoids are used as a preferred surface on which geodetic network computations are performed and point coordinates such as latitude, longitude, and elevation are defined (source).
- Ellipsoid Height
- The height of an object above the reference ellipsoid in use. This term is generally used to qualify an elevation as being measured from the ellipsoid as opposed to the geoid. GPS systems calculate ellipsoidal height (source).
- Geoid
- Earth's geoid is a calculated surface of equal gravitational potential energy and represents the shape the sea surface would be if the ocean were not in motion (source).
- Mean Sea Level
- Sea level is generally used to refer to Mean Sea Level (MSL), an average level for the surface of one or more of Earth's oceans from which heights such as elevations may be measured. MSL is a type of vertical datum – a standardized geodetic reference point – that is used, for example, as a chart datum in cartography and marine navigation, or, in aviation, as the standard sea level at which atmospheric pressure is measured in order to calibrate altitude and, consequently, aircraft flight levels (source).
- Ocean Surface Topography
- Measurement of the sea surface height relative to Earth's geoid. The height variations of ocean surface topography can be as much as two meters and are influenced by ocean circulation, ocean temperature, and salinity (source). I will not be concerned with these variations in this post.
- Orthometric Height
- The orthometric height of a point is the distance H along a plumb line from a point to the geoid. Orthometric height is for all practical purposes "height above sea level"(source).
Key Parameters
Figure 2 shows the relationship between the key parameters of mean sea level, ellipsoid height, and geoid height.
Analysis
Information Required
Here is the information that I need to gather:
- list of mountains taller than 5500 meters – my arbitrarily chosen limit – with their elevations.
- latitude and longitude for each mountain
- geoid correction factor for each mountain
Plan of Attack
The following list details my process for solving this problem:
- Gather a list of mountains taller than 5500 meters.
Fortunately, the Wikipedia has an excellent list of mountains in order of height. To use the database, I need to ensure that I have the mountain names in my list EXACTLY like they are in the Geonames database
- Write a VBA program to access the Wikipedia data.
Because a small number of Wikipedia geographic entries do not location data (i.e. latitude and longitude) in their database, I will need to flag these entries for manual lookup. I will simply leave locations with no latitude and longitude tied to the name blank. I can then search for blank entries to locate them.
- Look up the missing information using Google searches.
This was a bit slow because I had a difficult time locating some of the shorter mountains on the maps.
- Determine the geoid correction term using a utility available from the good folks at the National Geospatial-Intelligence Agency.
This program is fed a text file of coordinates and it gives you back the geoid correction to the ellipsoid used to approximate the Earth's shape.
- Compute the distance from the center of the Earth using a formula from this web site, which also does an excellent job deriving the formula.
I needed to convert Equation 1 into an Excel formula. Not hard, but you have to be very careful because long formulas in Excel are painful.
- Sort the list from most distant to least distant from the center of the Earth.
This gives me the result that I wanted, which I can compare to other sources on the Internet.
Gather the Data
Grab Latitudes, Longitudes, Elevations
I have written an Excel workbook that will obtain the latitude and longitude for the mountain names in my list of highest peaks. The workbook contains a VBA routine that will:
- read each mountain name from a table of names.
- send a request to the Geonames server for the XML data for that name.
- parse the returned text to separate out the latitude and longitude values.
- write the latitude and longitude values to the table column assigned to hold the return value.
About 10% of the mountains do not have an entry in the Geonames database. There are various reasons for this:
- Mountains like Annapurna have multiple peaks with names that are not in the Geonames database (e.g. Annapurna II).
- Some mountains are missing location data in the database (e.g. Guli Lasht Zom).
To run the routine, you must make sure that your VBA includes a reference to "Microsoft XML, 6.0". You need to go into the VBA IDE (Alt-F11), click on the Tools menu, and click on the References. You will see Microsoft XML, 6.0 there and you need to check it.
My routine runs when the button is clicked. The routine concatenates string versions of the latitude and longitude data using "|" as a delimiter. I can then use Excel's Text-to-Column function to separate the latitude and longitude. A bit crude, but it works well enough for this one-time instructional exercise.
The Geonames database requires that you have a user name. There is a cell in the workbook for your username. I have removed mine.
Compute the Geoid Corrections
Now that I have the latitudes and longitudes of the mountain summits, I can run a free tool, called intptdac.exe, to generate the geoid corrections. The program could not be any simpler to run:
- create a list, called Input.dat, with two columns of data
- first column contains latitude data (North positive)
- second column contains longitude data (360° format, positive going East)
- Run intptdac.exe
- A text file is created, called outintpt.dat, that has three columns: latitude, longitude, geoid correction.
Calculation of the Distance from the Center of the Earth
I have used Equation 1 that was beautifully derived on this web site to determine the distance from the center of the Earth.
| Eq. 1 |
where
- D is the distance to the center of the Earth [m]
is the latitude of the mountain summit [°]
- Z is the height above mean sea level [m]
- G is the geoid height [m]. Note that G is a function of latitude and longitude.
- a is the semi-major axis of the Earth reference ellipsoid (a= 6378137 m)
- b is the semi-minor axis of the Earth reference ellipsoid (b= 6356752.3 m)
Results
Table 1 shows the 28 mountains with summits furthest from the Earth's center. The spreadsheet has a much larger list of 210 mountain summits.
| Name | Latitude ( °) |
Longitude (°) |
Geoid (m) |
Elevation (m) |
Distance (km) |
| Chimborazo | -1.469167 | -78.817 | 25.96 | 6267 | 6384.4 |
| Huascarán Sur | -9.122 | -76.604 | 21.02 | 6768 | 6384.4 |
| Huascarán Norte | -9.1217 | -76.604 | 21.01 | 6655 | 6384.3 |
| Yerupajá | -10.267 | -76.9 | 25.64 | 6635 | 6384.1 |
| Cotopaxi | -0.6841 | -78.438 | 27.46 | 5897 | 6384.1 |
| Huandoy | -9.0273 | -77.6628 | 20.63 | 6395 | 6384.0 |
| Kilimanjaro | -3.0758 | 37.3528 | -16.26 | 5895 | 6384.0 |
| Cayambe | 0.029 | -77.986 | 24.45 | 5790 | 6384.0 |
| Antisana | -0.485 | -78.1408 | 26.06 | 5753 | 6383.9 |
| Siula Grande | -10.2947 | -76.8917 | 25.78 | 6344 | 6383.8 |
| Alpamayo | -8.8789 | -77.6536 | 18.96 | 5947 | 6383.6 |
| Nevado Pisco | -9.0016 | -77.6292 | 20.38 | 5752 | 6383.4 |
| Salcantay | -13.3336 | -72.5444 | 42.59 | 6271 | 6383.3 |
| Pico Cristóbal Colón | -10.838 | -73.687 | 27.24 | 5776 | 6383.2 |
| Coropuna | -15.5203 | -72.6572 | 43.61 | 6425 | 63823.1 |
| Janq'u Uma | -15.8533 | -68.5408 | 46.18 | 6427 | 6383.0 |
| Illampu | -15.8167 | -68.5333 | 46.02 | 6368 | 6383.0 |
| Illimani | -16.6539 | -67.7847 | 41.82 | 6462 | 6382.9 |
| Ampato | -15.8167 | -71.8833 | 44.08 | 6288 | 6382.9 |
| Nevado Sajama | -18.108 | -68.883 | 44.28 | 6542 | 6382.7 |
| Chachakumani | -15.9858 | -68.3817 | 45.83 | 6074 | 6382.6 |
| Wallqa Wallqa | -15.8167 | -71.8833 | 44.08 | 6025 | 6382.6 |
| Huayna Potosí | -16.2625 | -68.154 | 44.49 | 6088 | 6382.6 |
| Chachani | -16.1914 | -71.5297 | 43.28 | 6057 | 6382.6 |
| Parinaquta | -18.1667 | -69.15 | 44.5 | 6348 | 6382.5 |
| Pomerape | -18.1258 | -69.1275 | 44.51 | 6282 | 6382.4 |
| El Misti | -16.294 | -71.4090 | 43.09 | 5822 | 6382.3 |
| Everest | 27.9881 | 86.9253 | -28.73 | 8848 | 6382.3 |
I can confirm that the results for the first and last table entries (Chimborazo and Everest) agree with the Earth center distances given in the Wikipedia, which I quote below:
The summit of Mount Everest reaches a higher elevation above sea level, but the summit of Chimborazo is widely reported to be the farthest point on the surface from Earth's center, with Huascarán a very close second. The summit of the Chimborazo is the fixed point on Earth which has the utmost distance from the center – because of the oblate spheroid shape of the planet Earth which is "thicker" around the Equator than measured around the poles. Chimborazo is one degree south of the Equator and the Earth's diameter at the Equator is greater than at the latitude of Everest (8,848 m (29,029 ft) above sea level), nearly 27.6° north, with sea level also elevated. Despite being 2,580 m (8,465 ft) lower in elevation above sea level, it is 6,384.4 km (3,967.1 mi) from the Earth's center, 2,168 m (7,113 ft) farther than the summit of Everest (6,382.3 km (3,965.8 mi) from the Earth's center). However, by the criterion of elevation above sea level, Chimborazo is not even the highest peak of the Andes.
Conclusion
I was able to extract geographic information from the Geonames database and process that data to obtain a list of mountains furthest from the center of the Earth.
Appendix A: Workbook Link
Here is the link to my workbook.



Very nice article and I'm always learning something new from your articles. I used Bing Maps from Excel 2013 to graphically map your top 20 mountains, ref.:
https://www.dropbox.com/s/rouimxnbz3njwjk/Mark_Biegert_Top_20.png
I had uploaded a screen snapshot to Dropbox and shared it with all. Unfortunately, that link comes out as a boxed "X".
I forget to add to the post that you need to go into VBA and add a for reference Microsoft XML, v6.0. That may be your trouble. I will update my post.
mathscinotes
I just did another download of your Excel file and the VBA code is missing.
That is really strange. I have uploaded it again. It worked when I re-downloaded it. I would appreciate if you would try it again.
mathscinotes
The linked xlsm has the code as of 3 Jan 15 @ 7:57 PM Pacific
Thanks Ronan.
mathscinotes
The link is live. I clicked on it and it works.
mathscinotes
Pingback: Mississippi River and Its Distance from the Center of the Earth | Math Encounters Blog
What a fantastic article, which I stumbled upon while researching a blog post about Chimborazo, which I climbed earlier this month.
I don't understand a word of it, but I'm delighted to see that someone has proved mathematically that Chimborazo is indeed the highest mountain in the world!
I wonder if Mt Kenya would also make it onto your list of top mountains. At only 5199m in height it didn't qualify for your base data, but like Cayambe, the 8th mountain on the list, the Equator passes right through it.
Something tells me that you probably understood some of what I was doing. Basically, I used this problem as an excuse to learn how to use the Wikipedia as a geographic database. I need a problem to motivate my learning – I am fairly practical that way.
I will try to take a look at Mt. Kenya. No guarantees though.
mathscinotes
Pingback: Chimborazo: the furthest mountain from the centre of the Earth – Mark Horrell
Just an observation: why do you think that nearly all the top 28 are in the Southern hemisphere? (With the glaring exception of Everest, and, Cayambe which at just 2 miles North of the equator hardly counts as being in either.)
I would be speculating, but this image of the exaggerated geoid shape of the Earth may provide some insight.
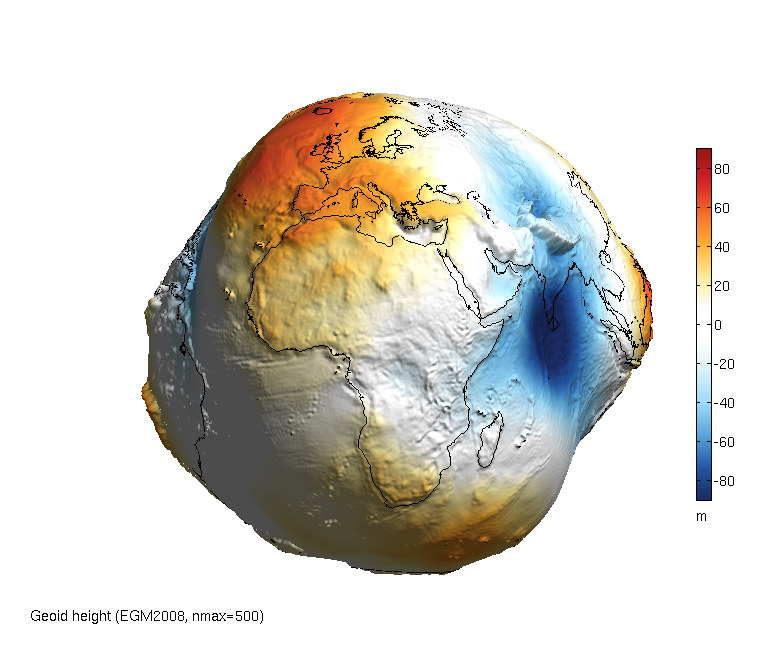
Ughh!
Sorry, I mean, Ahhh. Thanks
planeta asteroidiota
Pingback: Mount Everest isn’t really the tallest mountain on Earth | Times of Education
Pingback: Mount Everest isn't really the tallest mountain on Earth
Pingback: Mount Everest isn’t really the tallest mountain on Earth | E-Scientific News
te comento en español: te felicito por el fantastico trabajo, faltan algunos picos como el Nevado del Huila en Colombia que tiene 5365 msnm y se halla a 2 grados 56 minutos Norte, la misma latitud del Kilimanjaro, deberia ocupar el lugar que le corresponde, gracias,
Creo entender el problema.. la lista de montañas que utilizaste debia ser mas grande incluyendo picos de 5000 msnm
You are correct. Thank you for writing to me. I enjoy hearing from readers.
mark
pregunta : cuales son los dos puntos de la tierra mas distantes en linea recta ?, no es condicion que la linea pase por el centro de la tierra, propongo la linea entre el monte Cireme en Java y el Ritacuba blanco en Colombia, la separacion angular es inferior a 1 grado, problema de antipodas
Pingback: History Through Spreadsheets: Supreme Court Confirmations | Math Encounters Blog
Pingback: BrokenPla.net - The Important Eclectic News Syndicate
Pingback: Mount Everest isn't technically the tallest mountain on Earth - Science Global News
Pingback: Mount Everest isn't really the tallest mountain on Earth - LiveBrain.com
Pingback: Mount Everest isn't really the tallest mountain on Earth - Science News Hub
Pingback: Mount Everest isn't really the tallest mountain on Earth - Science News
Pingback: Mount Everest isn't really the tallest mountain on Earth - Weird Facts About Life
Pingback: Everest News
Pingback: ¿Cuál es la montaña más alta del planeta? Pista: No es el Everest y está en Latinoamérica - Nation
Pingback: Mount Everest isn't really the tallest mountain on Earth
Just came across this, and wondered if you could help with an extension of this math problem... I was curious as to what pair of points on the earth are furthest from each other. For antipodes, you could sum the distance from the center of earth, correct? How would you compute the distance between two points that are not exact antipodes?
I don't know how to calculate this distance exactly, but here is where i would hunt: knowing A. the earth is generally largest along the equator, and B that there are an array of peaks in the vicinity of Chimborazo that are the points furthest from the center of the earth, that is 1/2 of your answer.
If there were also C. another range of large equatorial volcanos very near to Ecuador's antipode (there is! https://en.wikipedia.org/wiki/Bukit_Barisan ) I would look along that Ecuador—Sumatra axis (perhaps Chimborazo—Gunung Kerinci) as a likely answer to your question.
The lay terms "elevation" or "altitude" imply height above sea level. Prominence implies height above key col. What is the term, if there is one, for earth's center to peak?
Good question! I don't know for sure, but I think it is geocentric distance. A related term is the geocentric radius, which is different because it is relative to a reference spheroid. In the case of the Earth, both would be close in value. However, distance is absolute and not with respect to a reference figure.
Thanks for the comment.
mark