Quote of the Day
Eggshells smashing each other with hammers.
— Winston Churchill, describing his feelings on battleship combat.
Introduction

Figure 1: Factors Affecting Range Ballistics. (Source)
I must admit that I am a bit of a battleship junkie. I have been reading some old US Navy manuals on battleship fire control, which discuss the various effects that must be corrected for to ensure accurate fire (Figure 1). In this post, I want to examine how the curvature of the Earth affected the gunnery direction. Curvature corrections are only needed for very long-range artillery.
Gunnery direction calculations usually begin with a range table (Figure 2), which tells the gunner the angle that projectile must be fired at to hit a target at a given range on the same horizontal plane as the gun (i.e. no difference in height between the gun and target). The target height relative to the gun can be either positive or negative, which affects the range that is used to index into the range table . For example, battleships in WW2 doing shore bombardment sometimes needed to attack fortifications on mountains (e.g. Mount Suribachi on Iwo Jima). For sea-level sea battles, the targets are below the horizontal plane of the ship firing the projectile.

Figure 3: Example Where Target is Lower Than
the Gun. (Source)
Figure 3 shows that firing at a target that is at sea level also involves a difference in heights. The rangefinders on a battleship determined a Line-Of-Sight (LOS) distance, but that distance is not the same as the horizontal distance listed in the table of Figure 2. The LOS distance must be corrected to an effective horizontal distance that can be looked up in the range table. My goal in this post is to show how we can correct the LOS distance to provide the required horizontal distance, which can then be used to read the gun elevation from the table in Figure 2.
All calculations are performed in Excel – my workbook is here.
Background
Earth Curvature Calculation
I have written about how to compute the curvature of the Earth over a given distance in another post using Equation 1, which relates the deviation from horizontal to the distance from the measurement origin.
| Eq. 1 |
where
- δ deviation from horizontal, which is called curvature in gunnery.
- R is the radius of the Earth (3963.2 miles)
- RLOS is the LOS distance.
These parameters are illustrated in Figure 5.
We can use Equation 1 to compute a curvature versus range table (Figure 4). This table duplicates the results shown in this reference.
To illustrate how to read this table, consider the range of 19,800 yards. We go to the row that corresponds to 19,000 yards and find the column that corresponds to 800 yards. At the intersection of the row and column, we find a curvature of 84 ft.

Figure 4: Table of Curvatures for Different Horizontal Ranges. This figure shows how to find the curvature for a range of 19,800 yards, which is 84 feet.
Rate of Height Change
The US Navy manuals refer to "Column 19" and the "Change in height of impact for variation of 100 yards in sight bar." While this sounds like a complex parameter, it is simply the tangent of the projectiles impact angle with respect to horizontal, which is called the angle of fall and is listed in the range table shown in Figure 2. The tangent of the angle of fall tells you how many feet the projectile loses in height for every foot of horizontal distance. We will use this parameter to relate the height difference to the range correction.
Analysis
Earth Curvature Correction Calculation
Figure 5 defines some variables using the illustration of Figure 3. You can see in Figure 5 hitting target on a requires reducing the range setting of the gun (RH) from the distance measured along the line of the sight (RLOS) by Δ, i.e. .
For modeling purposes in Figure 6, we can treat the trajectory of the shell near the target as a straight line. This allows us to use a simple trigonometric function to compute Δ, i.e. .
Example
I copied a section of the range table from the US Navy manual and used it to compute: (1) curvature; (2) change in height of impact for variation of 100 yards in sight bar (i.e. LOS range); (3) danger space (discussed in this blog post). I can verify that (1) and (2) agree with the manual. Item (3) is discussed but not listed in the manual tables.
Conclusion
I am interested in understanding the gunnery corrections for the Earth's curvature and the Coriolis effect. I believe this post thoroughly covers the curvature correction. I will put out a post shortly on the correction for the Coriolis effect.





earth is not curved. water is always measurably flat. earth is mostly water. therefore earth has to be flat
I am working to understand how the US Navy directed the fire of its now obsolete battleships – correcting for the Earth's curvature was part of their procedure. I do not plan on entering into any flat Earth debate here.
mark
smart man. you can never win an argument with a flat earther because they dismiss all logic or evidence that disputes their flat earth religion. although they believe they understand the science and math i have yet to see one that understood science past the high school level. in fact most understand at middle school level at best. this is based on my observations.
Aint related to marilyn are ya?
Wow! It’s like coming home from a naval battle, and some land-lubber tells you victory was in fact impossible using your calculations because the earth is flat. You can’t even take someone like that seriously.
I believe Matt was kidding and surprised to see how many comments were directed towards it. Similar to Greta Thunberg's Flat Mars Society that pokes fun at science deniers.
Though I understand there are approx. 1,800,000 Americans who honestly believe the Earth is Flat. I would ask them what's keeping the oceans from emptying ???
Great analysis of 16" ballistics
Its called an icewall buddy !! Your welcome ! Any more questions ?
You do realise Antarctica is a continent (roughly circular in shape) and is surrounded by water on all sides. We have seen the earth (and Antarctica) from space with photographs taken by astronauts, satellites and with live video feeds.
The earth has two sets of star trails, one in the northern hemisphere moving counter clockwise about Polaris and one in the southern hemisphere moving in a clockwise direction with totally different stars about a point which is NOT Polaris.
This would be impossible if the earth was flat and only possible on a rotating sphere.
And yet mr dumb dumb it has to be corrected for. UHF radio at sea level has a range of around 15 miles and yet on a mountain that is increased somewhat but you can transmit on uhf 4000 plus miles using a satellite tho get around the fucking curve. Radar has a longer range the higher up it is mounted but guess what can see an aircraft at 100 miles away but again navigational radar is around 15 miles.
If you are going to deny facts that's fine but is best not to publish your ignorance.
Yes it can also be easily explained why the horizon is flat laterally too !
You don't do yourself any favors by denying something even the ancient Greeks knew... Come on over to the truth. We have lots of cool facts and you too can belong.
We know the earth is round because the moon is round. It's in the bible too.
The Bible mentions the Firmament.
It doesn't mention it with relation to the Earth being flat, though.
That's a term taken out of context by the flat Earth fools
@Matt Almost a year and a half later and i still dont believe you re really that ignorant
Wrong, Matt. Water is not flat. Look at any drop of water on a table, it is round like a bubble. This effect is very obvious in beakers that have lines for measurement, where you can see that water has curvature.
This physical attribute of water and other fluids makes measuring them precisely with the lines a bit harder, thus easily and repeatably disproving the notion that 'water always finds its level'. (No, this does not change with bigger bodies of water.)
The earth is simply, far larger than you think.
Thank you, Mathscinotes, for sharing this with us, the math and visuals are brilliant.
I bet you 20 bucks that he cannot post any mathematical evidence to support his comment. The funny thing is that anyone who has taken high school trig can verify these equations.
Fucking retarded Flat Earth trolls.......if the earth was flat you could stand on Mt Everest and see Chicago, if the world was flat but it is not. Flat Earthers are fucking retarded fuck heads that could not pass high school science.
The Flat Eathers are one thing. You should see some of the things people say about me – and they don't even know me.
Bahaaaa thats impossible dident you see the news ffs theres no such place as Chicago silly nope no bulls nor blackhawks its all a MIRAGE thats rite boys and girls its a mirage
?? Best comment on the internet. ?? ???
Personally, I have no time for flerfs. These arrogant twats dropped out of high school, probably never passed a science test in their life and now have the audacity to pretend they are smarter than all the worlds experts in their relevant fields, simply because something doesn't meet their infantile expectations and childish intuitions.
Columbus was looking for alternate source of opium because the Indian trade route was closed. Not spices like you were taught in school.
Why when they could get opium from Kazakhstan, all the way down to almost saudia Arabia, without even crossing all the way over the kush region. Tea was from Asia cumin, paprika, etc. Were harder to find than poppies. Now Vietnam and laos in the 60s was opium war.. hence the 60s-70s heroin epidemic in america from troops shipping crates of china white back to the u.s.
We had similar problems to consider in field artillery. Our tabular firing tables included corrections for atmospheric density, powder temperature, target above or below gun, effects of cross wind and range wind, direction of fire, weight of projectile, and others. If a target was above the level of the gun, this necessitated a positive correction. Target below gun necessitated a negative correction. These corrections were called site, and could be obtained from the tabular firing tables or from a graphic site stick, somewhat like a slide rule. Site corrections were made for each charge, as most field artillery pieces have multiple charges available affecting velocity and therefor shape of trajectory. Firing due east required a slight negative correction, as the target was moving toward you. Firing due west required a slight positive correction because the target was moving away from you. Any other direction than due east or west the correction was somewhat less, determined by trigonometric calculations (done for us in the tables, as we were all DAGBYs: dumb ass gun bunnies!). The latitude of your position also figured into these calculations. We also had the cotangent of the angle of fall included in table G. Using this function, we could tell how close to the target in defilade a shell would burst if it just cleared the highest point (such as a building). This was useful in determining whether high angle or low angle fire should be used.
Hi Jim,
Thanks for your comment. It is good to hear from a practitioner. I am always amazed at the level of detail involved in these ballistic calculations.
My father was in the field artillery (specifically, fire control/communications). As a boy learning to shoot, my father taught me about angular measurement using mils and the effects of weather and gravity. We did not have much time together, and those are times I cherish.
mark
I was in the FDC for an m198 battery, United States Marine Corps. I know that this post is a couple of years old, and I stumbled upon it looking for the math and trig to refute an idiot flat earther, and I have to say I love this article and the comments!
Thanks for writing. Yes, some of the comments do get pretty interesting. My favorite posts are the ones on the old battleships.
mark
Dont worry about all that nonsense for trajectory an such just follow all military manuals ever printed and make your calculations to apply to a flat immovable plane look it up at the beginning of every flight manual ever printed ffs ! Your fake military documents are pathetic to say the least !! Prove me wrong ??
There were also more factors involved. Each individual gun had muzzle velocity variation corrections to apply, due to tube wear. Each gun tube had a maximum effective life. More rounds fired meant the muzzle velocity would drop due to tube erosion. This was taken into account using a chronograph to measure muzzle velocity averages during firing for each gun, and then applying a correction for the difference from a standard muzzle velocity. There was also gun displacement. As the trails of the howitzer were fired in, the gun would displace slightly and had to be accounted for. These corrections would be in tenths of mils of elevation that were applied using the gunners quadrant. Also the weather (METT) data would change and anything over 4 hours (really 2 hours) was considered outdated. Finally you could conduct some form of registration to determine did hit to should hit corrections. I am not sure if much of this is still taught in the digital world.
Great comment! I am still looking for an old photograph of a gun team that had a single row of people each one responsible for adding each correction. I have read that the German cruiser Prinz Eugen could actually measure the velocity of each round as it left the muzzle and make a correction. I am looking for that document also.
thanks.
mark
Wow your dumb is even dummer then his dummest
Hi Jim,
would you be able to explain to me the math involved in the ballistic trajectory? This one game has been giving me a serious headache because they won't bother to explain the aiming part.
Mark, thanks for a fun post. I've also been interested in battleships since I was a child. Looking forward to your Coriolis effect analysis.
I too have always been interested in battleships – they look cool. Also, I am fascinated as to how people can spend so much money on things that end up being of so little practical use. Battleships were produced at great cost, but in the end it was the aircraft carrier that was their downfall. Nuclear weapons are similar in that we have spent an enormous amount on them (US alone spent about 6 trillion dollars on them and is planning to spend more), but you cannot use them.
I have started on the Coriolis post, but stuck on some nagging details. I will get it done.
mark
Mark, I found this Maple worksheet which demonstrates the action of Coriolis force on a projectile launched from Earth in an airless environment. Also, the curvature of the earth is not taken into consideration in this worksheet.
https://www.maplesoft.com/applications/view.aspx?sid=1437
I modified it to print out the below information. I choose two bearings for a shot: one bearing due east; and the other bearing 45 degrees from North.
--------------------------------
Initial Speed: 650.00 m/s)
Elevation Angle Above Horizon: 55.00 degrees
Bearing from North: 90.00 degrees
Initial Altitude: 0.00 m
North Latitude of shot: 49.00 degrees
(x,y) Position without Coriolis effect (40512.26, 0.00)
(x,y) Position with Coriolis (40463.68, 240.26)
Time to position without Coriolis 108.66
Time to position with Coriolis 108.27
Range from origin to point without Coriolis: 40512.26 m
Range from origin to point with Coriolis effect: 40464.39 m
Distance and bearing from North to Coriolis point from point without Coriolis effect: 245.12 m, -11.43 degrees
Distance from Coriolis Point to a line going from origin to point without Coriolis effect: 240.26 m
---------------------------
Initial Speed: 650.00 m/s)
Elevation Angle Above Horizon: 55.00 degrees
Bearing from North: 45.00 degrees
Initial Altitude: 0.00 m
North Latitude of shot: 49.00 degrees
(x,y) Position without Coriolis effect (28646.49, 28646.49)
(x,y) Position with Coriolis (28502.02, 28743.01)
Time to position without Coriolis 108.66
Time to position with Coriolis 108.38
Range from origin to point without Coriolis: 40512.26 m
Range from origin to point with Coriolis effect: 40478.70 m
Distance and bearing from North to Coriolis point from point without Coriolis effect: 173.75 m, -56.26 degrees
Distance from Coriolis Point to a line going from origin to point without Coriolis effect: 170.41 m
If you wish, I could email you a copy of my work. Hopefully, my descriptions make sense.
I will try to take a look at your stuff shortly.
Also, I just came across this nice article on battleships on Quora that you might like.
https://www.quora.com/Why-have-big-battleships-e-g-USS-Iowa-and-the-Bismarck-become-obsolete-in-modern-navies/answer/Aaron-Layne-8
Sure you will lol no curvature dummy thsts why
Mark,
I downloaded your Excel workbook and found this minor typo in the "RangeCorrection" tab. You state: "Change in height of impact for variation of 100 years in sight bar." Hopefully, no one wants to wait for 100 years for projectile impact 😉
Cheers,
Ronan
Thanks Ronan! It is tough to proof your own stuff. I always appreciate your help on keeping the content clean.
File updated.
mark
Thank you for your comment. All those factors used to have to be computed by hand from tabular and graphic firing tables. Now, as I understand, it is all done by computer. Hopefully though some soldiers still know how to read a TFT and play charts and darts in case a stray bullet or shell fragment goes through the computerTHERE IS NO SUBSTITUTE FOR MANUAL BACK-UP!
Your comment on manual backup reminds me of a great news report I saw a couple of years ago. The universal application of GPS had caused the US Navy to the reduce the amount of celestial navigation taught to sailors. Now with the rise of anti-satellite technology and GPS spoofing, the US Navy has decided that they needed to ensure a manual backup navigation method was available.
I have always been fascinated by celestial navigation (and all primitive navigation) and it is a hobby interest of mine.
Thanks for your response.
mark
Mark, FYI Binkov's Battlegrounds, a Youtube guy, has a video on a theoretical engagement between the IJN Yamato and the USS Iowa at: https://www.youtube.com/watch?v=W3C_gicuoPw
Hi Ronan,
That is a good video. I need to try out World of Warships. The only game I play now is Silent Hunter III.
Thanks for the comment.
mark
I am not a mathematics expert, nor a ballistics expert, but I have a question, kind of back to basics. The longest recorded naval shot was on the Guilio Cesare hit by Warspite at 26,000 yards. From my understanding of WWII naval warfare, LOS or Line Of Sight was a requirement of ballistics, deviation from horizontal, etc. You show this in your drawing. You cannot aim at something that cannot be seen. Your chart clearly shows at 26,000 yards the Cesare would be 154 feet below the event horizon, or the curvature of the earth. The Cesare was approximately 100 feet tall to top of mast, approximately 75 feet to top of funnels. How can one calculate line of sight, or deviation from horizontal to a target that is completely obscured by the curvature of the earth? Magnification is not the answer, you cannot magnify something on the other side of a sphere that is blocked by the body of that same sphere. The best information I can find shows the Musashi, the largest battleship ever built was less than 154 above the waterline, much less a dreadnought class battleship almost 2/3 the size. How can gunnery make adjustments to splashes that are over the horizon of a sphere and not in sight? Take your picture showing curvature of the earth and plot it to scale with Warspite and Cesare. Cesare would be totally beyond the curvature, no Line of Sight is possible. Your Line Of Sight would go through the water. Now do your calculations.
Thank you for your question. I go through the details of the maximum optical range calculation in this blog post. The calculation assumes that the battleship rangefinder can only see the tip of the target mast. This scenario is illustrated as follows.
The Warspite's rangefinder height is nominally ~28 meters. I say nominally because it varies with the loading of the battleship. I will use your value of 100 ft for the mast height of the Giulio Cesare. The maximum range calculation is performed as shown below.
The HMS Warspite used 15-inch guns with a nominal range of 33,550 yards. So the max optical range and gun range are consistent.
My calculations produce similar results to those in this stackexchange post.
mark
How did you calculate hW and HC?
Also the mast of that era were about 90ft.
I suspect that Al Sidell is a flat-earther. Yes, they really exist. One of the many mistakes they often make is to confuse the so-called 'drop' of a target object (its distance below a horizontal line from the observer) with the amount (if any) of the target object that would be hidden behind the curvature of the earth. These are usually quite different things. At a distance of 26,000 yards - about 15 miles - the 'drop', for an observer at sea-level, would be about 8 inches times 15-squared, which comes to 150 feet. But for an observer on a ship at a height of, say, 50 feet above the sea, only about 20 feet of a target object at 15 miles would be hidden. So there is really no problem about the line-of-sight, even without appealing to spotters on planes or frigates etc accompanying the battleship.
Agreed. I have found numerous references to targets being optically tracked accurately out at 35k+ yards (one well-documented incident involves Iowa). The critical target data, like range rate and bearing rate, are easily computed by tracking the target for a reasonable period of time.
Thanks for your comment.
mark
Battleships used spotter planes launched from catapults to spot shots and splashes beyond visual range.
In response to Al Sidell, I wonder if there might not have been aerial spotters radioing the splash locations back to the Warspite. Your evaluation of the distance and visibility seem to ring true, so perhaps further research might show the presence of such aircraft (possibly "String bags", Faiery Swordfish). As i am unfamiliar with this battle, perhaps there were surface ships closer to the Caesare which could have radioed or otherwise signaled necessary corrections. Just a thought.
Hi Jim,
There were airborne spotters at the Battle of Punta Stilo. See this link for details. My response to Al's question shows that the Warspite and Giulio Cesare were within optical range during their engagement.
mark
Hi Jim,
One more comment. The splashes can be seen from an amazing distance. Here is a Youtube video showing how high the splashes rise from the USS New Jersey. They are easily seen from the ship. Of course, the New Jersey's gun in this video were at low elevation, but you still can see the size of the splash.
mark
Perhaps there were spotter aircraft for splash marking, anything is possible. That does not explain how the initial firing solution was derived at without line of sight. You may not be familiar with this engagement, but there are many cases for such long range shooting. The Sharnhorst fired at HMS Glorious at 26000 yards. The Glorious was a converted heavy cruiser to aircraft carrier. Her overall height would be less than a Battleship of the same era, or less than the Cesare. Pictures show what looks to be the same funnel after conversion, the Cruiser super-structure was removed(above the funnel) during conversion. So lesser height above the waterline than the Cesare, built within 6 years of each other. So you have about same range with the target being even smaller and further behind the curve of the earth, according to your chart. There must be an explanation to arrive at the initial firing solutions. An initial firing solution cannot be made with spotter aircraft, or without line of sight, direction and range. Forgive me, but, I cannot fathom a person discussing, in depth, naval targeting, gunnery, and all the intricate details and mathematics of WWII naval gunnery, and not knowing anything about the longest shots taken in battle in Naval history. They would seem to be of the most interest of all. I bow to the mathematician for an explanation.
Hi Al,
I hope my previous responses provide you sufficient explanation. To summarize:
By the way, I am not a mathematician. I am an electrical engineer with experience in designing military hardware. I simply like to use simple math to explore problems that I encounter every day.
mark
As long as we are discussing amazing battleship engagements during WW2, I do want to mention the performance of the USS West Virginia (Wee Vee) at the Battle of Surigao Strait. Here are the points about this engagement I would like to highlight.
I am taking nothing away from Warspite – it holds the range record. Both WeeVee and Warspite show that the old WW1 battleships could still perform well during WW2.
mark
The Scharnhorst's hit on HMS Glorious and the USS Massachusetts' hit on the French destroyer Fougueux might dispute that record.
Scharnhorst hit Glorious from over 26,000 yards, as analyzed here:
http://www.navweaps.com/index_tech/tech-006.php
And Massachusetts claims a hit (and sinking) of the Fougueux at over 26,000 yards as well.
So that record is kind of disputed, especially by Scharnhorst since multiple ships were shooting at Fougueux.
Not to take anything away from Warspite, but the record is certainly in dispute or at least, shared.
There's also some modern analysis that suggests Yamato hit one of the escort carriers off Samar at 30,000 yards.
So silly... No coriolks effect ever measured to aim any weapon targeting system ever... Seriously, read any military weapons manual ever and you will not find coriolis effect mentioned. Also, you proved the earth to flat twice in your article without noticing. Firstly, the measurement of the deviation from the horizon has NOTHING to do with curvature. It calculates the difference between the elevation of your position and the target, that's it thats all, no curve. It can go either way up or down and even when your target is at higher elevation there is no adjustment for curvature... That is to say once you make the Calc for deviation from horizon and adjust your weapon to hit a target at higher elevation you would then need to adjust again for curvature but this doesn't happen... Because there is no curvature.
Secondly, your calculations using the radius of earth should alert you. Considering sea levels and land elevation the actual radius of the earth as relevant to your position would change with each Calc. Why doesn't this happen? Because the number is totally arbitrary and simply allows one to use trigonometry, representing a triangle, which has three NON CURVED lines... Let that sink in... You have proven the earth flat without any question.
BTW I am a mechanical engineer in the CAF not an uneducated goof I have studied flat earth for 4 years and not once have I ever been able to find one proven contradiction to a flat earth despite the fact I thought it was ridiculous at first.
> "No coriolks effect ever measured to aim any weapon targeting system ever... Seriously, read any military weapons manual ever and you will not find coriolis effect mentioned."
In terms of artillery manuals. You'll find them in most. Take for example Eugene Slover's publication of the USN 16"/50-caliber Mk7 gun operational manual's figure for the characteristic ballistics of the gun.
> "irstly, the measurement of the deviation from the horizon has NOTHING to do with curvature. It calculates the difference between the elevation of your position and the target, that's it thats all, no curve."
This notion is based on what exactly?
> "Secondly, your calculations using the radius of earth should alert you. Considering sea levels and land elevation the actual radius of the earth as relevant to your position would change with each Calc. Why doesn't this happen? Because the number is totally arbitrary and simply allows one to use trigonometry, representing a triangle, which has three NON CURVED lines... Let that sink in... You have proven the earth flat without any question."
Please elaborate.
> "
Totally false that no coriolis effect was accounted for, for long range gunnery.
It's absolutely taken into effect. In fact, they considered which way they were firing...into the rotation of the Earth or with it. They had to remember which hemisphere they were in. They actually had different tables for just that, which you can easily find.
All this was accounted for. One only has to google "coriolis effect naval gunnery" to find numerous links to info and discussion of just this and how it was accounted for.
https://eugeneleeslover.com/USNAVY/FC-APPENDIX-B-8IN-55.html
In fact, from Eugene Lee Slover's page, here is an actual firing table for an 8" US Naval gun. It literally says:
"Effect in yards of range due to rotation of the Earth"
So yeah, they knew about it and it was already built into the tables. The crew didn't have to calculate it on the spot.
Once again, I am no expert, I am just a disabled navy veteran, and became fascinated by WWII naval battles 40 years ago while in service. They had a plethora of naval history in the ships library. I would like to make a couple of observations though. I was wrong when I stated the top of the mast on Cesare was approximately 100 feet. I can't find exact measurements for either the Warspite or Ceasare, what I have found is that most estimates are hugely over concerning a ships height above the water, even my own. The height above the water for a Nimitz Class aircraft carrier is 60 feet, which really surprised me, as I have been on board the USS Enterprise. It is so huge I guess one loses a sense of scale. Which vastly over shadows WWI vintage battleships(both were built around 1917). Therefore I cannot cede you the 28 meter or 90 feet height for the rangefinder. Also, anti-aircraft rangefinders were mounted high on the super-structure, usually above the funnel, gunnery rangefinders were mounted very much lower, almost always on the gun batteries themselves, this is verified by Colin Vass who built an award winning scale model of the HMS Warspite. Each main battery had it's own rangefinder mounted on the battery itself. I cannot measure exactly, but the Warspite draft is listed at 33 feet, that is where the waterline is painted, at nominal draft, draft can vary with loading, but it is a very good baseline. The turrets where the rangefinders were mounted according the model, is almost equal distant from the waterline as is the keel, I would say certainly not more than 40 feet from the waterline. In battle conditions most ships were fully loaded with fuel and armaments, which if anything would lower the rangefinder relative to the water. Naval gunnery control in WWII used almost exclusively stereoscopic rangefinders, which used parallax to determine range, not very complex. What is interesting is these instruments not only provided the range to target, it provided the targets speed and course, all requirements to formulate a firing solution. Here is a quote concerning the use of this instrument. "Measuring the target's speed and course was considerably more tricky than range. It required a combination of looking at the orientation or angle of the target's superstructure and profile along with its bow wave and wake, to determine a base course or angle. Then, how fast it moved across the field of view of the range finder to determine a base speed using the angle of a base course and time mathematically. Also included was how the bearing to it changed as you observed it, taking into account your own ships speed and course. " So, it may or may not be true the top of the mast was visible through magnification alone, a firing solution was not possible using only the mast. According to the documented usage and instructions of the instrument, and appreciable view of the target ship is required for a firing solution. You can verify this information independently. We MUST limit capabilities to what existed at the time for the purposes of this discussion. If the methodology used at the time required viewing a super-structure, profile and even perhaps bow wave and wake for computation, one cannot assume otherwise at this point. Especially in view of the accuracy involved in the engagement. Cesare opened up at a reported range of 29,000 yards and within 3 minutes bracketed Warspite. According to my website, the curvature of the earth is 179.36 feet at 16.4 miles. Given the rangefinder is approximately 40 feet above the water, 139.36 feet of the Warspite would have been obscured by curvature which is more than double that of the USS Enterprise. Seeing as Warspite returned fire at near the same distance, the reverse is true, 139.36 feet of the Cesare was obscured. So the line of sight issue becomes even more pronounced. There are numerous examples of naval gunnery commencing well in excess of 30,000 yards, no hits however, but amazing accuracy never the less.
Just as a curious side note, the rangefinders in use were the very best available at the time, great effort and expense were expended in the research, development and design by some of the most learned and intelligent people available.
Curious question, why would they include bow wave and wake in the computation? According to all available information today, the bow wave would have been obscured within approximately 9,000 yards or five miles due to curvature of the earth, even less for smaller ships and wake probably less than a mile. Five miles is a mere chip shot for naval gunnery. One would assume they knew that. Just a curious thing.
Sidell: Therefore I cannot cede you the 28 meter or 90 feet height for the rangefinder.
I have done some searching for main battery nominal director heights and here is what I found.
Height (m)
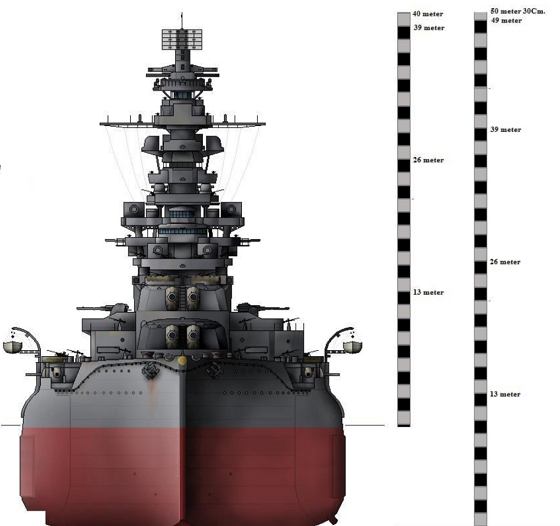
If you need see an example of where I found this data, the Iowa data is from the USS Iowa Crew Handbook. As you can see, 28 m is not unreasonable at all. Here is an excellent illustration from the Wikipedia of the battleship Fuso that illustrates just how tall a run-of-the-mill battleship was. The main battery directors are at ~35 m.
Sidell: Here is a quote concerning the use of this instrument.
The function you are describing used to be called rangekeeping. I wrote a Wikipedia article about this subject years ago. A critical part of rangekeeping involves determining the rates of range and angle change. WW2 rangekeepers were sophisticated analog computers that were capable of determining these rates using an iterative process. This process required initial estimates of the angle on the bow and target speed. Poor estimates would work, but it took longer for them to converge to a firing solution. There are great stories of people like Dick O'Kane spending hours practicing determining the angle on the bow by using a Lazy Susan, IJN ship models, and a reversed binocular to shrink the image to the size seen through a periscope. He supposedly got so good he could reliably determine AOB within 1° (reference).
Target speed was estimated using various methods. Submarine skippers used hydrophones to measure the prop rotation rate and translate that value into speed (reference). Surface ships would use the size of the bow wave to estimate the speed. It was not a great method, but it was close enough for a rough estimate. While not describing surface ship fire control, Dick O'Kane did a wonderful job describing the iteration process with respect to torpedoes in his book Clear the Bridge!.
I do not have a good reference for how a surface ship director is used operationally, but I do have the following Youtube reference that discusses how a torpedo director worked. Their operation was similar.
Before I spend too much more time on this, did you review my reference to my post on how refraction affects rangefinding? This article discusses how the line-of-sight (LOS) is not straight.
mark
Hey Mark,
I love your article. A Japanese acquaintance I made on Google+ when that was still a thing had collected numerous photos and details of Yamato/ Musashi design I would like to get you these details if you so wish. I need his permission to post them here, but I have a majority of stuff saved.
Again, great work.
I know, how about this. The Warspite used "over the horizon" rangefinding like found on the later Iowa class battleships, and used its 18.1 inch main turret to make the shot, just like the Yamato had. Why not? It seems its other characteristics are totally comparable. Never mind that the Warspite, A Queen Elizabeth class battleship built in 1913 was 244 feet shorter than the Iowa, I am sure its height was equivalent and characteristics were the same. I will check the silhouette cards for WW2, I am sure the Warspite, Iowa and Yamato are virtually identical, its a wonder we didn't sink our own ships. Even though the most casual reference to the Warspite history shows that prior to the engagement in question, its main mast, you know, where the spotting tower is, was removed to make room for a crane and hanger deck for amphibious aircraft. You remember, the Warspite, the ship that made the shot, the topic of discussion. Not the Iowa, not the Yamato, the Warspite. How does that effect your mast to mast calculations? As to that, can you provide ONE documentable instance of any ship in WW2 obtaining a firing solution from a mast alone? The documentation is astounding detailed. Yes, I am aware of refraction, I am aware it MAY increase ones line of sight by refracting along the curve of the earth, also I know it MAY refract away from the surface and reduce ones line of sight also. It also MAY not be there at all. It all depends on a lot of variables. Which you seem to assume were present and in the direction you desire for your math to work. I also tire of the discussion, all you are interested in is the mathematics, just prove your mathematical theory. You have accepted no information I have provided about the configuration of the Warspite, perhaps it doesn't work in your model. Perhaps a wholly different class of ship does fit your model. Actual historical, provable facts seem to have no bearing on your mathematical theory. I think it best if I just go back to my naval history books and you go back to your calculator. I would offer one word of caution, there is no natural law or scientific law that states the universe or even our world must conform to or agree with mathematics. It mostly seems to, but there is no law. Mathematics is a construct devised by humans. Perhaps Tesla was correct.
Al Sidell - "Perhaps Tesla was correct"? In what way Al?
In thinking AC was the way to distribute electrical power? I think he was right there.
In not believing in the existence of electrons? No, without electrons there would be no microelectronics and we wouldn't be using the internet!
I knowing that the Earth is a globe? "...Nearly two years after I had flashed an electric current around the globe, Edison, Steinmetz, Marconi, and others declared that it would not be possible to transmit even signals by wireless across the Atlantic. ..." (Nikola Tesla, A Machine to End War Liberty, February 1937).
Oh, YOU mean the misquote so often used by deceptive Flat Earthers! See https://flatearth.ws/tesla-misquote and you will find yet more FE dishonesty at work.
Re. HMS Warspite's range finder height above the waterline after refitting. The height of the stack is 79 feet above the waterline; the rangefinder is placed atop the citadel or armored bridge, above the stack. I apologize for not providing documentation, other than illustrations with the height of the stack quoted, but can we say 10feet? Yes, there are rangefinders on the turret- for wayward destroyers and cruisers, and land bombardment. But WTF are you folks goin' on about? It's engineers vs. mathematicians. What difference does it make when a 2700 projectile, either armored or explosive, rips off your head and turns the rest of you inside out? Check out Drachinifels website, "Why did the Hood sink so quickly?" Of course, the world is flat. As far as you can see.
You can see the director atop the bridge structure in WWII here.
It's not as high as a typical US BB, but it's much higher than the turret.
And we can keep in mind, they couldn't see the entire ship of an opponent a long way away. They could see the top of it though, and they could see their shell splashes, as they were taller than even a Battleship.
https://i.imgur.com/c7AQbMa.jpg
Not sure how to start this - all elements of the Battleship Fire Control and Gun system are aligned to the Fire Control reference plane with physical offsets - called Parallax entered into the Fire Control computer as part of the ships design. Testing and refinement of this alignment is done with Battery Alignment using stars as targets. The LOS range is modified by the ballistic cam in the computer/rangekeeper too compensate for the earths curvature and spin. These cams are unique, having be developed using actual gun firings along the Potomac River at NSWC Dahlgren VA.
You are correct about the use of ballistic cams. They were used to represent one and two-variable ballistic functions. These were remarkable mechanical devices. They were so complex to manufacture that the first numerically-controlled machine tools were developed to manufacture the 3D units. These machines drilled holes to precise depths into a slug of steel.





A human machinist then filed the slug smooth to reveal the final shape.
Here is what the final cams looked like (2D and 3D).
Here is how a 2D cam was used in a simple director.
Here is how a 3D cam was used in a more complex director.
Thanks for your comment.
mark
No, the Tesla quote I was referring to is as follows, "Todays scientists have substituted mathematics for experiments, and wander off through equation after equation and eventually build a structure which has no relationship to reality." I tend to agree with the man. I am just pointing out how facts are changed to fit the theory or math. Look at the explanation for the Warspite hit. Main battery fire control up on the mast or super-structure, when it was not, even later generations like the Iowa had its main battery fire control on the battery itself. Secondary battery and anti-aircraft fire control were high on the super-structure. But the height is required to make the math work. The Warspite had it's mast removed to make room for the aircraft cranes prior to the engagement. The use of refraction to see the target over the horizon, as if refraction was a constant, it is clearly not. Mast to mast line of sight required to make the math work, while fire control of the time required much more data to formulate a firing solution than the mast. Not one historical example of mast to mast calculations having been even attempted much less used. Every conceivable variable put into place to make the math work. As a last resort, reams of calculations that only an Einstein could possibly refute. As I go through life I continuously see these anomalies. What you can see, touch, hear or taste is not real, because math proves it is not. According to science, we live in a continuously expanding universe, everything is moving away from the center, where the "Big Bang" occurred. The earth orbits the sun at about 67,000 miles an hour, our solar system is moving at 490,000 miles an hour, everything in the universe is moving at speeds that are hard to fathom, all in different directions. Yet the North Star, Polaris and the constellations remains in a constant position or orbit throughout human history. Interesting, is it not? I would like to see the math on that! The anomalies are simply ignored in deference to the theory. I read an article last week concerning the hole in the ozone, in 2016, it was the largest it has ever been since it's first observation. The article went on to explain how the banning of aerosols have worked and the hole is healing. Really? Well you see, the scientists have found the way we were measuring it was incorrect, and according to the new and improved measurement it really is getting smaller. HUH? You change the yardstick then say the measurement is now how you predicted it would be? Even though using the same measurement techniques used previously, the hole is bigger, we can rest assured it is healing, I suppose because they said it would heal, and the scientists are always correct. Want a math problem? One that goes against preconceived ideas of human history? Do the math on the Great Pyramid. Today, in 2018, it is still taught that the pyramid was built during the reign of Khufu, about 25 years. There are approximately 2.5 million stones in the pyramid, do the math. 100,000 stones per year, 1,923 stones per week, 274.7 per day, 11.4 per hour, approximately 1 stone every 5 and a half minutes. Quarried, moved, shaped to exact measurements, fitted to exact standards every 5 1/2 minutes with bronze tools and manual labor. 24 hours per day, seven days per week for 25 years. I wonder, could we build it today given these time parameters, even with our modern technology? It is still taught today that the pyramids were burial chambers for the kings or pharaohs, what is strange is the fact that no bodies or mummies have ever been found in a pyramid, ever, not even previously unopened ones. Where was King Tut found by Carter? In the Valley of Kings, why is it called that? It is where the have found the bodies of the kings. Strange is it not? Curious indeed. Science says, when the facts do not agree with your premise, re-evaluate your premise. I guess that part of science has been dumped into the dustbin of history. Science has never been about consensus. The greatest scientists in history went against the preconceived and accepted truths of the day. They proved the consensus to be wrong. There is the notion that the universe works on math, it appears to in most all cases, but math is a human construct, developed by the human brain, the universe was not. Mathematically and aerodynamically explain why a Bumble Bee can fly? Mathematically it cannot. The explanation? No one ever told the bee it couldn't fly, so it does. Another anomaly passed over by science and math. For decades science stated the 4 independent wings of a dragonfly was what enabled it to fly backwards, couldn't be done with 2 wings. Then they filmed a hummingbird flying backwards, no explanation, just a curiosity. I just find life curious.
FYI, Iowa's (and every other US Battleship from about WWI forward) had their main battery directors in the superstructure. The director optics on the turrets were redundant units, not the main director at all.
And I thought I had given this response awhile back. I receive updates from this thread by email, but I don't see a post of mine here that I'm nearly sure I made.
Anyway, hope this clears up the director issue for the US ships.
Naval artillery tables absolutely included the Earth's rotation, curvature, etc, in them. This is beyond debate.
First off, mathscinotes, NOTHING but appreciation for your excellent blog and love of all things WW2, especially battleships. I am actually working on my own design of a BATTLE OF MIDWAY board game featuring miniatures and dice. I love reading about WW2. I am 49 and grew up watching John Wayne movies and building plastic models with my older brother. Good times. Please do not take my comments from here forward as anything mean or cruel. I happen to be a staunch Christian, Bible Thumper, and a Flat Earther. I drove tanks in the US Army National Guard for 6 years and have been teaching Elementary School Art for 24+ years.
Now the gunnery images on his blog DO NOT come from WW2 documents. They are from a SAN FRANCISCO MARITIME NATIONAL PARKS ASSOCIATION pamphlet created to LOOK like it was old, with 'MONOPOLY STYLE" WW2 era illustrations. They have attempted to create a NOSTALGIC look to their MODERN document which DECEIVINGLY incorporates their GLOBE even into the front cover. You can view the ANACHRONISM here https://maritime.org/doc/firecontrol/partc.htm
Funny, if you look at what appears to be the ACTUAL WW2 manual reference chart (source cannot be determined) it has NO calculations for CURVATURE. However, it DOES mention PLANE.
https://i2.wp.com/mathscinotes.com/wp-content/uploads/2017/12/RangeTableExample.png
I would like to see an ACTUAL WW2 document which shows a calculation for curvature, not some modern San Francisco pamphlet designed to APPEAR to be old. Thanks again for your great interest in all things WW2.
Final note, Al Sidell, you are just too cool. I love your posts here.
First, PLEASE tell me when your board game is finished. I have a son who is a board gamer and it would give us something to play together. Second, I welcome everyone to comment – just keep the discussion respectful and civil. You would be amazed at what I have to filter.
As you can tell, I love battleships and WW2 history. You are correct that range tables always being referenced to an infinite plane. Where I differ from you is that I believe that curvature is always applied as a correction. The reason for delaying the correction is because both the battleship and land target may be at different heights. So on curvature, we will have to disagree.
As far as contemporaneous publications that discuss curvature corrections, see "Physical Bases of Ballistic Table Computations, Ordnance Textbook – United States. Army. Ordnance Dept" dated 1919. I refer to this document because it is public domain (i.e. free), available on Google Books, generated by the Army, provided the calculation basis for subsequent decades, and is pretty readable. It also does a nice job with the Coriolus correction.
Thanks very much for writing. I also appreciate Al Sidell. I welcome comments from you both.
mark
https://www.amazon.com/Battle-Pivotal-Moments-American-History/dp/0199315981#
Here is the link to the INCREDIBLE book on the Battle of Midway. Filled with eyewitness accounts and IN DEPTH character profiles of US and Japanese Commanders. INCREDIBLE read. My brother and i would hang out in our deceased father's woodshop and discuss massive passages i read to him. Best book on the topic ever. how can i post and send pictures of my game as i develop it? i will show you what i have so far and would value any criticism. it is NOT my goal to hijack your blog here and go off on a Flat Earth tangent. Someone in a FE duscussion durected me here. Now back to Midway... Is there a way to attach images if snap some? using my PHONE today. i prefer TYPING on my computer.
Powered by Cricket Wireless
Craig Symonds is the author of this book. He is one of my favorite Civil War authors. It does not surprise me that he would write a first-rate book on Midway. Check out CSPAN's BookTV. He occasionally gives lectures that are covered there. His lectures are excellent.
I would love to see some images of your board game. I am not sure the best way to proceed. You could put them on Flickr or Instagram with a comment here that includes a link.
mark
Mark,
You SUSPECT I am a flat-earther? So this suspicion invalidates any questions I raise? It is now science and math policy to only answer questions from "acceptable people"? So it would make a difference if I was an atmospheric scientist when I point out that refraction is not a constant and cannot be used as such? Then would the statement be valid? Only then would it be the truth? Would it make a difference if I was a naval architect and pointed out how the size, dimensions and pictures of several classes of larger and newer battleships was researched and provided to prove the math, while the size, design and modifications to the actual battleship was ignored, while readily available. Would the statement be valid and true only then, because of who I am? Are my questions to be ignored because I MAY be black, bi-sexual, or from Somalia? Do you have a current list of who is allowed to ask scientific or math questions? Do you SUSPECT that everyone who realizes that the North Star, Polaris, has remained in a constant position throughout human history is a flat-earther? Gee it was in my fifth grade SCIENCE book. Refraction being a variable is also in the science books. I did not write them, I did not make this up out of thin air, I simply read the science books. This is how I formulated the questions. Is everyone who knows that Bumble Bees cannot fly, aerodynamically, a flat-earther? I did not read this in any flat earth literature, I read it in a SCIENCE book. Truth be known, I have not read any flat-earth literature at all. However, I now, may. Science is fascinating, what is even more fascinating to me are the anomalies that are simply not explained or ignored. Einstein replied, when asked about a panel of scientists and mathematicians convened to disprove his theory, "No amount of experimentation can ever prove me right, a single experiment can prove me wrong". Which takes me back to my quote from Tesla about math vs experiments.
Mark said NOTHING about you being a Flat Earther … that was DavidB. I did agree with the calculations in the comment made by DavidB.
mark
Al, I think you are a flat earther, because you repeat the same myths and lies that are peddled by the flat earth community!
You say, '...the Tesla quote I was referring to is as follows, "Todays scientists have substituted mathematics for experiments, and wander off through equation after equation and eventually build a structure which has no relationship to reality."' Tesla was WRONG! He was a 19th century experimenter unable to come to terms with the progress of the 20th century. If he had been right that electrons don't exist, then the microprocessors which we are using for this exchange would be impossible! The "mathematics" of quantum physics and relativity have been proven BY EXPERIMENT and are used all the time today.
You ask, is "everyone who realizes that the North Star, Polaris, has remained in a constant position throughout human history is a flat-earther?" That is simply untrue! Ancient astronomers did NOT see Polaris in the same position we do - a FE myth!
What about "everyone who knows that Bumble Bees cannot fly, aerodynamically" - not true, another myth!
And you finish with a false Einstein quote, which is exactly the OPPOSITE of what he did say (see https://www.quora.com/Did-Einstein-actually-use-the-phrase-No-amount-of-experimentation-can-ever-prove-me-right-a-single-experiment-can-prove-me-wrong”).
You are not scientifically curious, you are scientifically ignorant and have easily fallen for the deception spread by the FE community.
The FE movement came from two places , first almost everything we are taught is a lie and from Nasa. As a spectator to all this , I can say that either side has proven their arguments as both are theories and difficult to prove. Then, I got to thinking the Yamamoto could lob a shell 26 miles. That means the shell at maximum range would be 45 degrees elevation would apex at 13 miles. The drop of the earth would be 17 feet roughly. That got me to thinking that there must be a ballistics correction for the curvature of the earth based on these two arcs for battleships. The world record shot is now 5000 yards. That takes a lot of math. Sniper 101 aka TiborasarusRex on You Tube covers these calculations in great detail. This one consideration both sides have ignored.
Note a scientific theory is defined as an explanation that has and can be repeatedly observed, verified, and consequentially proven. A theory in a legal or general sense means essentially the same thing as a scientific hypothesis. It's just an idea. But for an alternative or a disproval of a standing scientific theory to occur, concrete evidence has to be brought forth. FE's have no consistent model. Period.
Jack, FYI, the below website talks about the Paris Gun from WWI. For a long-distance shot with air resistance, a 45-degree elevation does not give the longest shot.
"These experiments uncovered what appeared at first sight to be a strange result: that maximum ranges are best achieved at elevations of around 50 to 55 degrees, not the 45 degrees that geometry (and ideal conditions in a vacuum) would suggest. The reason, Krupp’s technicians quickly appreciated, was that the earth’s atmosphere grows thinner the higher the altitude. Consequently, at the higher elevations, a long-range shell is traveling for a greater part of its trajectory through very thin air, increasing the range. This phenomenon would be significant for the Paris Gun project."
This first test-fire of the Paris Gun had it's shell go about 20% farther than anticipated and outside of the German Gun range onto private property.
http://www.astronautix.com/p/parisgun.html
This comment section made my day. 🙂
To mathscinotes: Great blog! Thanks for all the hard work, data, and info; made a great read Saturday afternoon.
To Al S: Best laugh I've had in a while, keep it coming whenever you check here again *thumbs up* you guys are great.
Bob: you're a real patient hero. good stuff.
To anyone who hasn't seen this yet: https://himawari8.nict.go.jp/
Mark, I went back to refresh my memory (need an upgrade... Borg implants?) and noticed some typos:
1. In your RangeCorrection tab at B14, you state 17300, it should be 17500.
2. In your above Figure 7, you mention years rather than yards. You had fixed this in your workbook but not in this article.
Thanks for your interesting articles
Thanks Ronan! I just made the corrections. Sorry to take so long.
mark
Thank you so much for sharing.
Pingback: Earth’s Curvature and Battleship Gunnery | Math Encounters Blog | jtveg's Blog
Mathscinotes,
It is obvious that you have more than a junior high educational ability, There For, thank you for the scientific and mathematical rationale.
Digressing a moment from battleship gunnery and considering hunting rifle gunnery (ranges from a few feet out to 1000 yards), let's address the problem of uphill/downhill shooting. It's a fairly well accepted fact that there is a tendency to miss high when shooting at steep up or down angles. Referring to the latest post on the necessity of determining the actual HORIZONTAL distance to the target (That is, the measured linear distance you would see on a flat map showing the positions of the target and the gun.) there is a way to correct for this. Now, if you have a coincidence type or laser range finder you may range a target at, say for instance, 1000 yds-but your target is at a fairly steep angle above or below you. Let's say further that you accurately estimate this angle to be 45 degrees (up or down makes no difference). Where do you aim, or how do you set your sights? In this case you would click your scope or iron sights to your setting for 700 yards and be right on target. Simple, right? Oh, yeah; how did we arrive at that? The actual horizontal map distance between your gun and the target is THE COSINE OF THE ANGLE OF ELEVATION OR DEPRESSION TIMES THE LINE OF SIGHT RANGE. The cosine of 45 degrees is .707 (call it .7). .7 times 1000 is 700. Now all you have to do is memorize a few cosines for say, 10 degrees, 20 degrees, 30 degrees, 45 (.7), and perhaps a few more and become proficient in estimating angles, and your good to go. By the way, don't forget windage! Happy shooting!
Hi Jim,
Years ago, I wrote a Wikipedia page on the Rifleman's rule. It was my first Wikipedia page and crude. However, I derived the exact form of the Rifleman's rule on that page. Here is a link. Hopefully, that provides a bit more background on why it works.
mark
The only thing flat earthers fear, is sphere itself.
That is very cute!
mark
Hey, flat earthers have members all around the globe
How boosting ships in World of Warships?
World of Warships is the most popular arcade naval game where each player becomes the captain of the ship. WoWs forces you to incorporate strategy and planning before heading into battle. With well-developed maps, several ship classes and continuous improvements, each battle in World of Warships is a unique experience in the game world. You can plunge into the atmosphere of exciting battles and become a real professional.
Often, novice players try in WoWs account boost themselves. Beginners usually lose in their first battles, which affects statistics, and as a result, experienced teams do not take them to play. But besides this situation, you may encounter difficulty passing the ranking season. We can help you in any given situation together with our WoWs boosting services! This is not only a great chance for beginners to boost their account from scratch, but also a convenient opportunity for all players to do in WoWs what they like best without losing time.
WoWs boost is moving around the levels of development in a game to gain access to various game functions, as well as gaining a wows ranked battles higher level rank that assesses combat skills and team play. In this case, the player can receive various types of rewards. Our team can perform the most complex tasks that you cannot perform for any reason: boosting statistics or rating, farm credits or experience, upgrades and much more.
Sounds a bit spammy there.
WoWs is a great game. Not historically accurate, as far as the gameplay goes, but the ship models are fantastic, and there's currently nothing better if you want to drive a ship and shoot at other ships.
Please do the Coriolis effect article - My mothers uncle was a gunnery instructor on the HMS Hood - (he left after its grand world tour) - He was a very deaf man !!!
When he joined the home-guard in WWII the sergeant ask him what sort of gun he had used - I expect you used shotguns ? - No - Sir - 15 in. !
I hope you can tell me how much you would miss, if you fired at a target 15 miles away (the longest hits in ww2, as I know of) and did not take the Coriolis effect into account.
First of all, clarify that my native language is Spanish, but I will try to make my English as understandable as possible.
Congratulations Mark. The blog is very entertaining and educational, however I have a question, when the table says “curvature”, it refers to the fall with respect to the horizontal of the boat, but it does not apply to LOS, correct?
Reading the comments I realized that Mr. Al Sidell is a hopeless and ignorant flatearther who deliberately tried to adjust the numbers to his mystical belief each time he was answered. By the way, I don't know what his website is or what calculator he used, but his calculations are also heavily wrong, even Mike tried to correct his comment, but there was no case. What if I am going to do to prevent the atrocities of it from spreading, and I am going to leave links to two reliable curvature calculators.
The first is simpler and easier to handle for any user. It works in a geometric way, that is, it does not assume refraction or others: https://dizzib.github.io/earth/curve-calc/?d0=0&h0=0&unit=metric
The second, although more advanced, also allows for simple calculations. Although its great utility lies in the fact that all kinds of factors can be added to represent any type of real-life situation, in addition to offering a visual representation:
http://web.archive.org/web/20191017052939/http://walter.bislins.ch/bloge/index.asp?page=Flat-Earth:+Finding+the+Curvature+of+the+Earth. Remember that if the object is not visible in the visual representation, there is an option to use the zoom.
Well, with that said, I urge any reader in doubt to put in the observation height, distance and size of the object that Mr. Sidell points to in his answers (and that constantly changes to fit his theory) and check that there is no no problem with curvature.
By the way, before I get to my real question, I would like to clarify that a Nimitz-class aircraft carrier does not have a height of 60 feet above the water, that is ridiculous. The 60 feet are up to the flight deck, in total it measures about 134 feet (40.8 meters) above the water line.
Anyway, reading the Sidell comments made me wonder. I am aware that the Warspite's batteries each had their rangefinder, but when one reads about the Warspite, one mentions the existence of other elevated rangefinders; however, according to him they are anti-aircraft rangefinders. My question is: there was some substantial difference between battery rangefinders and anti-aircraft rangefinders that prevented the latter from being used to determine the position of an enemy ship, or at least provide data to formulate a solution for Shooting? In other words, it seems ridiculous to me that since early detection of the enemy's position is so important, the rangefinders with the longest range of the entire battleship are limited only to detecting aircraft.
In fact, I was reading about the fire-control system of the German Bismarck a few days ago, and although it was much larger than the Warspite, what it said caught my attention. Specifically, it mentioned that the four turrets of the main battery operated with the stereoscopic rangefinders of three command posts around the battleship (one of which was 31 meters above sea level), and in case it happened that the command posts were They were disabled in combat, each torrera had its own rangefinder to operate individually. Really the only reason I think the rangefinders at the command posts were preferred is because they offered more range of vision by being higher.
Here I attach the link in case someone is interested in reading: http://www.kbismarck.com/controltiri.html
I think Mike has brought up the subject of anti-aircraft rangefinders in another post, maybe he knows the answer. But from my point of view and since, as far as I understand, they work on the same principle, I cannot find a reason why the elevated rangefinders of the Warspite could not have been used to determine the position of the Cesare with a better range of vision.
Greetings, and if anyone knows anything about it, I would be very grateful for any input.
Regarding Warspite, and other Battleships, for that matter:
Yes, it had a central FC director. You can look up pics of her to see it. The turrets also had their own. These were backups. Navies like lots of redundancy.
But you wouldn't be able to get a solution for a long a distance with the rangefinders on the turrets, as they are not mounted as high as the main directors, but they do work fine otherwise.
Also, yes you can use the AA directors as FC for the main batteries, too. More redundancy.
Pingback: Feedback solves the Mars problem - MetaSD
I find it laughable that the people in this article are so sure their view is correct. Flat or round we have people that comment but fail to recognize that this subject has never been publicly debated by the expert from both sides. In fact one English Engineer posted a substantial purse if NSA or other designated authority for a round earth would come forth to do so. That was several years ago but still nobody has come forth to claim the free money. I wonder why they refuse to do so. I can think of only one reason.
There's no such thing as an "expert" in flat Earth, because the Earth isn't flat.
We know this beyond any doubt, so there's no "debate" to be had.
To even acknowledge such a fallacy by entering into a debate gives it credence that it deserves none of.
It's really amazing that in this day and age folks are so gullible as to fall for this nonsense.
A simple test would be to get two artillery guns capable of hitting targets at 20 miles distance, one crew comprised of Ball Earthers and one crew comprised of Flat Earthers. Have them both aim due west and zero their guns on a target exactly 20 miles away until they're both satisfied they can hit the target unerringly, on a flat plain. Then have the Ball Earthers relocate 10 miles east and have the Flat Earthers relocate 10 miles west, so that they're now exactly 20 miles away from each other. Then have them both fire at each other. If the Earth isn't rotating then they'll hit each other. If the Earth is rotating then only the Flat Earthers will die and, thus, STFU.
Mark, I came across a humorous picture of a flat-earther surfing championship. It's titled "40 People Missing After First Flat Earth Surfing Championship." I've uploaded that image to my Google drive. If you think it's appropriate, please add it to my post and remove the below Google drive link.
Hope You Had a Happy New Year,
Ronan
https://drive.google.com/file/d/1TDd_-40P9tRjQ9PgdemdbiY0MIP95mqW/view?usp=sharing
I did have a happy new year. I hope all is well with you. What really makes me happy is seeing that the cold looks like it is beginning to abate in Minnesota. Also, I am getting ready to go down to Florida for a week with some friends.
Good Humor on Flat Earthers! ... You cannot believe how many of these folks read my blog. I don't get it.
mark