I live in Minnesota, where owning a cabin on a lake in the northern half of the state is part of the culture. Here is a picture of my little piece of northern Minnesota.
My Little Northern Minnesota Cabin
My cabin sits on a small hill about 15 feet above the lake. Unfortunately, the hill is rather steep and a bit difficult to negotiate, particularly for the older folks. At this point, there is only a dirt path up the hill. To add to the difficulty, the dirt path is strewn with rocks and tree roots that make it even more difficult to scale. We thought about looking for a cabin in another location, we even found prefab cabins for sale online, but decided against it when we started talking about making our cabin more accessible.
One of my friends lives in Australia and has recently had a small granny flat built on his property and is also currently in the process of making it more accessible for his elderly relatives. He originally was going to build a cabin, but decided to upgrade to a granny flat instead. There are a fantastic range of cheap granny flats out there, so if you are thinking of building one on your land, make sure to do some research to ensure you get the best deal for your money.
As for my cabin though, I need to build a stairway between the lake and the top of the hill. This project is quite different from building a staircase indoors. In all honesty, I'd probably just use a professional like Pear Stairs if it was! Since summer is just about over and I do not use the cabin in the winter (brrr!), this will be a project for next spring. This means that I have some time to design the stairway. I will have several blog post on this design effort. For today, I will be looking at the basic design equations for a simple, straight flight of stairs.
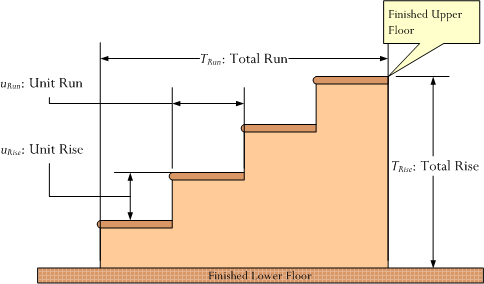
Let's begin by illustrating four key stair terms using the following figure.
Illustration of Some Key Stair Design Terms Used in This Blog Post.
The definitions of these four terms are given in the following list.
- TRise : Total Rise – The total (finish floor-to-finish floor) height of the stairs.
- TRun : Total Run – The total horizontal distance occupied by the stairs.
- uRise : Unit Rise – The rise of a single step of the stairs.
- uRun : Unit Run – The horizontal distance occupied by a single step of the stairs.
The Stair Design Process
The basic process of stair design is straightforward.
- Measure the Total Rise
- Calculate the Number of Risers
- Calculate the Unit Rise
- Calculate the Unit Run
- Calculate the Total Run
Measuring the Total Rise
The total rise of stairs is the one stair parameter that is generally fixed right from the start. However, there is some room for error. While the rough flooring-to-rough flooring height is fixed, the steps must be designed to provide equal riser heights after the finish floors are installed. This means that you have to obtain accurate estimates of the heights of the finish floors at both the lower and upper levels of the stairs before they are installed.
We can illustrate the measurement and estimation processes using the following figure.
Estimating Finished Floor-to-Finished Floor Height
We can compute the finished floor-to-finished floor height, TRise, using the following equation.
where TRoughRise is the rough floor-to-rough floor height, 
Calculating the Number of Risers
Most cities are adopting the International Residential Code (IRC) for the construction of single-family residences (often with some modification). This code states that the maximum riser height is 7.75 inches. However, I personally find a riser height of 7.75 inches to be rather high (some local areas allow a unit rise as high as 8 inches). A good nominal maximum for most people is 7 inches, though a shorter maximum may be more appropriate for facilities occupied primarily by children or the elderly. The IRC has no minimum riser height – it allows all the way to zero (i.e. a ramp).
where N is the number of steps and ceil is the ceiling function, which always rounds up. This approach ensures that unit rise is always less than or equal to 7 inches.
Determining the Unit Rise
Once you have N and TRise, determining the unit rise is easy.
For ease of measurement, you may wish to round the final result to a value that is convenient to measure (e.g. a multiple of 1/8 of an inch).
Determining the Unit Run
Determining the unit rise seems to be confusing to folks. I believe this is because there are some options as to how you compute it. There are three commonly used equations for calculating uRun given uRise, which I list below.
Equation 1:
Equation 2:
Equation 3:
The equations may appear complicated but really they are simple. Basically, you select a uRun that makes at least one of the equations true. The range of k values allows you to use values for the unit rise and unit run that are convenient to measure (e.g. multiples of an 1/8 or 1/4 inch).
These three equations actually produce similar results. To illustrate this point, consider the following graph. I made the graph by setting k equal to the mid-point of its allowed range for each of the equations.
Graph of Stair Angles Versus Equations and Riser Height
There are a few points that are worth making about the graph:
- The stair angles range from 30° to 44°.
- Equation 1 produces a stair angle that is less steep than the other equations for unit rises greater than 7 inches.
- Equation 2 and 3 produce stair angles that are less steep for unit rises less than 7 inches.
At a unit rise of 7 inches, all the equations produce stairs with the same angle or slope. At all other unit rises, each of the equations produces slightly different angles. The differences in angles can be useful when trying to fit a stairs into a specific total run.
Determining the Total Run
Once we have uRun, determining the total run of the stairs is straightforward.
The total run of stairs is important because it tells you how much of your lower level space the stairs will require. There frequently is some iteration required to get a workable combination of unit rise, unit run, and total run that fits in the allotted space and people can comfortably climb.
Conclusion
This blog post covered the basic math. Real stairs usually include some complications. For example, the IRC does not allow you to have a stairs with more than 18 steps without a landing. This requirement will figure prominently in my cabin stairway. In one of my stair blog posts to come, I will go through the actual numbers associated with my cabin stairs.
I don't know about the lack of minimum height for a riser. I have a friend who has post polio problems. She has problems climbing stairs. They wanted to redo the steps out the back of their house to have a rise of about 3 inches. They had to fight pretty hard to get an exemption for this. I wondered why they were so short the first couple of times I went there. It finally dawned on me it was so she could climb the stairs on her own.
Good comment. Here is a link that discusses the issue. Many localities have a minimum riser height specification (often 4 inches). The International Association of Certified Home Inspectors requires 4 inches as the minimum riser height. I don't know why the International Residential Code went down the path they did, but there is no minimum. Most communities are working toward conforming to the IRC.
Pingback: I Stumbled Upon Some Math Today… | PTC
Great article.How would you go about calculating the dimensions when building a Spiral Staircase? Any help would be appreciated!
My wife and I have actually discussed spiral staircases. I will see if I have any material that would be worth blogging about. I must admit that I find stairs (all kinds) very interesting from a design standpoint.
Thanks for the question.
Mathscinotes
Pingback: Stairway Rise Angles | Math Encounters Blog
Pingback: Layout Formula for a Balustrade | Math Encounters Blog