Projectile Time of Flight/Distance Versus Velocity

Posted on 26-February-2011 by mathscinotes

Introduction

As I mentioned before, I am reading the book "Modern Practical Ballistics" by Pejsa and am finding some interesting material there. I previously duplicated Peja's derivation for a function describing a G7 standard projectile's velocity versus range. This post will briefly look at functions for time of flight and range. I recommend going straight to the Pejsa book for those wanting a deeper dive into the subject. Note that Pejsa strictly uses imperial units. I will continue to use those units here, but the Mathcad routines shown are setup so that they will work with metric units as well.

While this derivation is centered on the G7 standard projectile, the results can be applied to a general projectile through the use of the ballistic coefficient. I will go through the details of this adjustment in a later post.

Analysis

Background

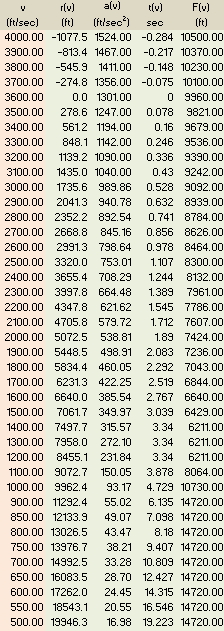
In my previous post, I only addressed velocities above 1400 feet per second (fps) to keep the functions simple. Pejsa actually addresses velocities all the way down to zero. After thinking about it, I decided it would be useful to show how one could express a complicated function in a computer algebra system, like Mathcad. Figure 1 shows the function that Pejsa uses for the entire range of velocities. This function is based on polynomials fit the G7 drag data.

Eq. 1

This function is represented by a Mathcad program. Using this acceleration function, I have generated a table of acceleration values versus some velocity values. This same table of data is in the Pejsa book.

Derivation of Time of Flight Formula

As discussed in a previous post, the acceleration of a projectile is modeled by Equation 2. Note that the exponent is modeled by 2 - n. This has to do with the drag coefficient being defined with respect to v2.

Eq. 2 a(v)=\frac{dv}{dt}=-k\cdot {{v}^{2-n}}
\frac{dv}{{{v}^{2-n}}}=-k\cdot dt\Rightarrow {{v}^{n-2}}\cdot dv=-k\cdot dt
\int\limits_{{{v}_{0}}}^{v}{{{v}^{n-2}}\cdot dv}=\int\limits_{0}^{t}{-k\cdot dt}
\left. \frac{{{v}^{n-1}}}{n-1} \right|_{{{v}_{0}}}^{v}=-k\cdot t
\frac{{{v}^{n-1}}-v_{0}^{n-1}}{n-1}=-k\cdot t
\therefore t=\frac{{{v}^{n-1}}-v_{0}^{n-1}}{k\cdot \left( n-1 \right)}

The value of the exponent correction n varies with velocity range as shown in Table 1.

Table 1: Drag Equation Exponent Corrections.
Velocity Range n
(exp correction)
0 fps < v ≤ 900 fps 0.0
900 fps < v ≤ 1200 fps -3.0
1200 fps< v ≤ 1400 fps 0.0
v > 1400 fps 0.5

Using Equation 2 and Table 1, we can derive a function for the time of flight (Equation 3).

Eq. 3

Distance Versus Velocity

A similar analysis can be done to obtain a distance versus velocity equation and table of data. Equation 4 shows the derivation.

Eq. 4 a(v)=\frac{dv}{dt}=-k\cdot {{v}^{2-n}}
\frac{dv}{dx}\cdot \frac{dx}{dt}=-k\cdot {{v}^{2-n}}
\frac{dv}{dx}\cdot v=-k\cdot {{v}^{2-n}}
\frac{dv}{dx}=-k\cdot {{v}^{1-n}}
\int\limits_{{{v}_{0}}}^{v}{{{v}^{n-1}}\cdot dv}=\int\limits_{0}^{x}{-k\cdot dx}
\left. \frac{{{v}^{n}}}{n} \right|_{{{v}_{0}}}^{v}=\frac{1}{n}\cdot \left( {{v}^{n}}-v_{^{0}}^{n} \right)=-k\cdot x
\therefore x=\frac{1}{n \cdot k} \cdot \left( v_{^{0}}^{n}-{{v}^{n}} \right)

Equation 5 and Table 1 allows us to generate the corresponding Mathcad program and output results. These results duplicate the results from Pejsa for a G7 projectile.

Eq. 5

Conclusion

Figure 1 summarizes all the data generated above, plus adds the data for F. The exact same table is at the back of Pejsa Chapter 8. Notice how I used an Excel component to allow me to format the table.

Figure 1: Generated Full G7 Data Table.

Figure 1: Generated Full G7 Data Table.

This entry was posted in Ballistics. Bookmark the permalink.

5 Responses to Projectile Time of Flight/Distance Versus Velocity

  1. David says:
    8-October-2011 at 4:19 pm

    I may have an error, but when running the >1400fps equation I don't get the same values as your table. In order to match your table values, I must replace the constant 166, with 189.5 (roughly).

    I'm using Excel, rather than Mathcad, so precision might be at fault, but the difference seemed larger than I'd expect from that.

  2. David says:
    8-October-2011 at 4:33 pm

    Oops, unclear which table I meant above - this is for retardation 'a'

  3. David says:
    8-October-2011 at 11:47 pm

    And another oops, disregard above... I had a messed up conversion constant (0.348 rather than 0.3048 to convert ft/s to m/s). All good now (embarrassed)

  4. Fernando says:
    10-March-2014 at 9:59 pm

    Am I missing something here? For velocities below 400 ft/s n=0, so Equation 4 would blow up to infinity. Is there a typo in Table 1?

    • shrink says:
      25-July-2014 at 3:34 am

      Actually, it wouldn't blow up to infinity, because you get an expression of the 0/0 type. Formally, it's a limit which has to be analyzed (e.g., by L'Hospital's Rule): it comes out that the limit exists and is equal to -1/k*ln(v/v0).

      Alternatively, you could come to the same result by integrating the left side of Equation 4 for n=0, i.e., calculating the integral of dv/v from v0 to v, of which the result is obviously ln(v/v0).

Comments are closed.