Trigonometry, WWII Torpedoes, and a Museum Docent

Introduction

I received a message a few weeks ago from a docent at an East Coast museum. He was using an article I wrote for the Wikipedia years ago to demonstrate an application of trigonometry to high school kids. In that article, there was a figure that had a typo in it and he wanted it corrected so he could use it for his class. Since my Wikipedia writings have primarily been about military history, I was a bit surprise that he was using material I created to teach trigonometry. We traded some emails, I corrected the typo, and what he was doing turned out to be interesting. I decided it was worth covering here.

Background

The Wikipedia article I had written was about torpedo fire control during World War II. The docent was creating a simulation of World War II submarine combat in an effort to provide an exciting experience for kids that involved history and trigonometry – two of my favorite subjects. The kids would be able to get a feel for the difficulty of what their great-grandfathers were trying to do nearly 70 years ago. It's always fun trying to explain what they would have to go through to calculate the measurements needed. It often startles them to learn that it wasn't as simple as using a calculator to aid them with their calculations. Calculators weren't created until the 1960s, and even then you wouldn't be able to search for graphing calculators reviews by bestcalculators.net since the internet didn't exist either. You would have to work out everything you needed by hand and mental math. So, understanding trigonometry was paramount to make sure your calculation wasn't incorrect.

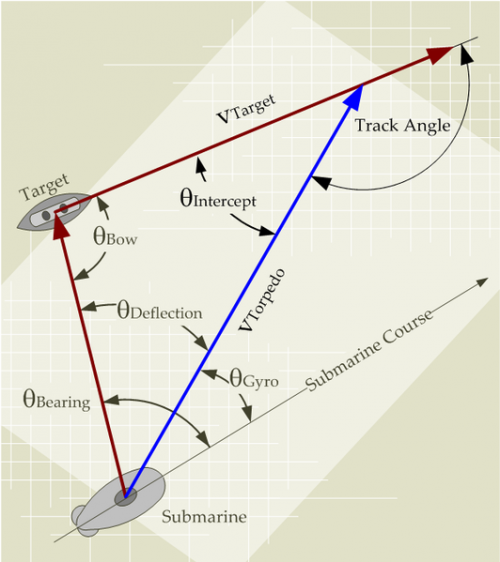
To understand the fire control problem, we need to define some terms. Figure 1 provides a visual illustration of the World War II torpedo fire control variables.

It turns out, that Figure 1 also illustrates the fire control problem. Equation 1 shows the equation that World War II sub skippers had to solve. If you look closely, it is a restatement of the law of sines.

Eq. 1
	substitute

• v_Target is the velocity of the target.
• v_Torpedo is the velocity of the torpedo.
• ?_Bow is the angle of the target ship bow relative to the target bearing.
• ?_Deflection is the angle of the torpedo course relative to the target bearing and is the critical value we are computing here.
• ?_Track is the angle between the target ship's course and the torpedo's course.

These old torpedoes ran on a straight line that was determined by the angle, which we compute using Equation 2.

Eq. 2

where is read from the submarine's compass and was computed by the Torpedo Data Computer (TDC), an analog computer built to solve Equation 1.

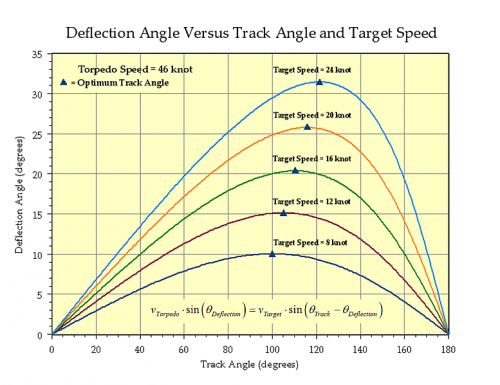
Just like the TDC, we can solve Equation 1 for versus to generate Figure 2. This is the figure that had the typo the docent wanted corrected. The typo of my original figure was in the equation that I had included as a note.

I originally saw this curve in the Submarine Torpedo Fire Control Manual. Sub skippers were told to try to fire with track angles at the optimum values, which are marked by small triangles in Figure 2. It was difficult for sub skippers to get an accurate estimate of the target ship's course , which was used to compute . The optimum track angle is where the curve is flat, which means that the impact of errors in are minimized.

Conclusion

You never know where your work will turn up. When the docent finishes his simulation, I am going to travel to the East Coast and try it out.

If you are wondering how I ever got interested in this subject, it is a long story that goes back to my childhood. One critical part of the story involves the book "Clear the Bridge" by Richard O'Kane. I consider that book the finest description of World War II submarine combat that I have ever read (and I read them all). Admiral O'Kane's writing has a lively style that made quite an impression on a teenage boy.