The Power of a Simple Magnifying Glass

Introduction

My favorite radio program is Science Friday. Last week, their web page included an excellent video where Science Friday's resourceful intern, Flora Lichtman, gave a wonderful explanation behind the use of a lens to concentrate the Sun's power. Her assistant in this effort was Thomas Baer, Executive Director of the Stanford Photonics Research Center (i.e. big shot). Here is a link to the video.

http://www.sciencefriday.com/embed/video/10380.swf

During the demonstration, they did bit of math that showed how a person could compute the level of solar power concentration provided by a simple magnifying glass. In a manner totally appropriate for this kind of video, they magically pulled out an equation and a value for the angular diameter of the Sun (Flora did say to look up the angular diameter of the Sun in any physics textbook). I thought it would be worthwhile to derive both the equation and the angular diameter of the Sun. Let's dig in ...

Analysis

During the video, Thomas Baer wanted to give a simple, approximate formula for the concentration factor of solar power provided by a common magnifying glass. He gave the formula shown in Equation 1.

Eq. 1

where F is the F-number of the lens. The F-number of the lens is defined as , where f is the focal length and D_Lens is the diameter of the lens. For the lens in their example, they computed an F-number of about 3.16, which means the concentration factor is 1000. This means that the power at the spot is the same as what entered the lens, but it is concentrated on an area 1000 times smaller.

I want to derive Equation 1 from first principles. We can start with Figure 1, which illustrates the geometry of the situation.

Figure 1: Illustration of the Magnifying Glass Scenario.

Determination of the Angular Diameter of the Sun

Figure 2 illustrates how to calculate the Sun's angular diameter at the Earth (Ө). I used Google to get the Sun's diameter (D_Sun) and distance (R_Sun).

Figure 2: Mathcad Screen Capture of Solar Angular Diameter Calculation.

This analysis agrees with the value listed in the Wikipedia.

Concentration of Solar Power From First Principles

Figure 3 shows my calculation for the magnifying glass' concentration of solar power. I make the assumption that we can approximate the diameter of the spot by using , where Ө is the angular diameter of the Sun.

Figure 3: Mathcad Screen Capture of Magnifier's Solar Concentration.

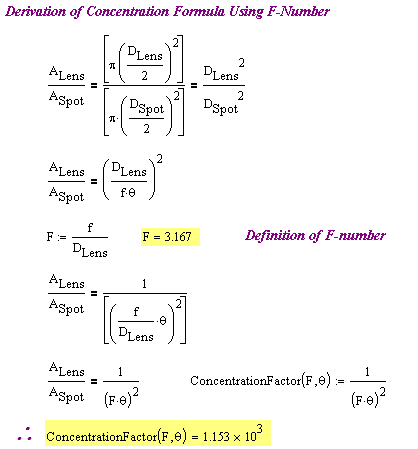
Concentration of Solar Power Using F-Number

Figure 4 shows my derivation of Equation 1. It is straightforward and gives the same numerical answer as above. The only difference from what Flora and Tom obtained occurs because my angular diameter is a bit different than theirs. Of course, they were using approximate numbers.

Figure 4: Derivation of F-Number Equation.

Conclusion

Flora and Tom did a nice job on the video. I wanted to walk through it and make sure that I understood mathematically what was going on. I believe that I do.

P.S.

If you want to see what you need to start a leaf on fire with a lens, see this post.