Solar Photons

Posted on 4-June-2011 by mathscinotes

Quote of the Day

Forgiveness is the final form of love.

— Reinhold Niebuhr

Introduction

Figure 1: Our Sun. (Source)

Figure 1: Our Sun. (Source)

I was watching "How the Universe Works" on the Science Channel and they had a really interesting discussion on stars and photons. During the show, they mentioned that photons generated in the center of the Sun take 4000 years to get to the surface. From the surface, the photons only take 8 minutes to get to the Earth. As part of my campaign to promote active television watching, let's take a look at where these numbers come from. As part of this effort, I will use Mathcad for the calculations and as a programming tool for a simple simulation.

 

8 Minutes to Earth

This is an easy one and Figure 2 illustrates the calculation. In this calculation, dAU is the distance from the Sun to the Earth, and c is the speed of light.

Figure 1: Confirmation of 8 Minute Transit Time.

Figure 2: Confirmation of 8 Minute Transit Time.

4000 years to the Surface

I had to think about this one a bit. I want to treat this like a Fermi problem (i.e. an exercise in rough approximation). Basically, a photon in the center of the Sun has to play a game of pinball with all the atoms in there on its way to the Surface. The classic way to model this situation is as a random walk. Let's look at how we can model a random walk process.

Random Walk Modeling

For simplicity, let's assume that we can model the photon as traveling an average distance l between each interaction with an atom. When a photon interacts with an atom, it is re-emitted in a random direction. I will ignore any time associated with the re-emission. Since it is a photon, it travels at a velocity c between the interactions. The mean distance, \overline{d}, that a random walker travels from its point of origin is given by Equation 1.

Eq. 1 \overline{d}=l\cdot \sqrt{N}

where

  • l is the length between interactions.
  • N is the number of interactions.
  • \overline{d} is the mean distance traveled.

We can derive this expression for the one-dimensional case as shown in Equation 2. For this case, the random iterates all have equal magnitudes, but random signs.

Eq. 2 d={{l}_{1}}+{{l}_{2}}+\cdots +{{l}_{N}}
\left\langle {{\overline{d}}^{2}} \right\rangle =\left\langle {{\left( {{l}_{1}}+{{l}_{2}}+\cdots +{{l}_{N}} \right)}^{2}} \right\rangle
{{\overline{d}}^{2}}=\left\langle {{l}_{1}}\cdot {{l}_{1}}+{{l}_{2}}\cdot {{l}_{2}}+\cdots +{{l}_{N}}\cdot {{l}_{N}}+{{l}_{1}}\cdot {{l}_{2}}+{{l}_{1}}\cdot {{l}_{3}}+\cdots +{{l}_{N-1}}\cdot {{l}_{N}} \right\rangle
{{\overline{d}}^{2}}=\sum\limits_{i=1}^{N}{\underbrace{\left\langle {{l}_{i}}\cdot {{l}_{i}} \right\rangle }_{={{l}^{2}}}}+2\cdot \underbrace{\sum\limits_{i\ne j}{\left\langle {{l}_{i}}\cdot {{l}_{j}} \right\rangle }}_{=0}=N\cdot {{l}^{2}}
{{\overline{d}}^{2}}=N\cdot {{l}^{2}}
\therefore \overline{d}=l\cdot \sqrt{N}

We can illustrate how this equation works with a simple simulation.

Equation Verification Through Simulation

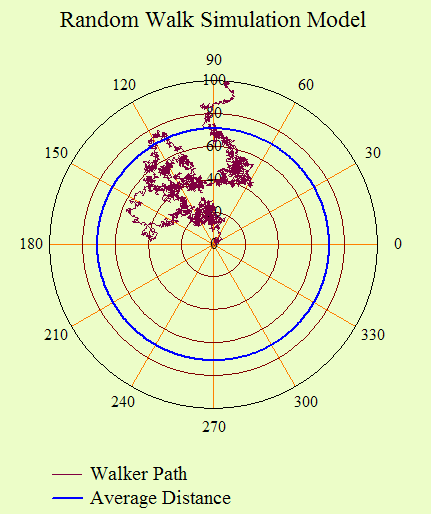
Figure 3 shows a Mathcad program for simulating a two-dimensional random walk of 5000 steps (variable N) 100 times (variable n). I will not go into detail here, but the results for 1, 2, and 3 dimensional random walks are the same.

Figure 2: Mathcad Simulation of a Two-Dimensional Random Walk.

Figure 3: Mathcad Simulation of a Two-Dimensional Random Walk.

The simulation uses complex numbers to make the path vector easily rotatable. I have set the interaction distance l to 1 for the demonstration. Figure 4 shows the result of one of trials from the program in Figure 3.

Figure 3: Simulation Results from a Single Trial.

Figure 4: Simulation Results from a Single Trial.

For 500 trials of 5000 interactions, the simulation computed a mean random walk distance of 69.4, while theory predicts 70.7 (Equation 1). The agreement is pretty good.

Solar Transit Time Calculation

We can compute an estimate for a photon's solar transit time as shown in Figure 5, which shows a simple pair of equations being solved simultaneously. In this system, I first solve for the number of interactions N. The transit time \tau can then be computed by assuming the photon traveled a distance of N \cdot l at a speed of c. For our rough analysis, we will assume that the average free path, l, for a photon is ~1 cm. Determining this number is complicated and I will refer you to this reference.

Figure 4: Calculation of the Transit Time for A Photon Through the Sun.

Figure 5: Calculation of the Transit Time for A Photon Through the Sun.

My result is ~5000 years, which is close to the 4000 years stated in the program.

Conclusion

I was able to derive the results stated in the program and got a feel for some of the dynamics going on inside of the Sun. All of the numbers associated with the Sun are so large that they always leave me in awe.

Save

This entry was posted in Astronomy, General Science. Bookmark the permalink.

2 Responses to Solar Photons

  1. Alan Stevens says:
    6-June-2011 at 7:33 pm

    Very nice, but a couple of corrections needed.

    1. Fourth line of equation 2: I think the N multiplying the second summation should probably be a 2. e.g. (l1+l2+l3)^2 = l1^2+l2^2+l3^2+2(l1.l2+l1.l3+l2.l3)

    2. You've been a little fortunate in your simulation of 5000 random steps. The "distance" to compare with the square root of 5000 should be a root mean square distance, not a mean absolute value (which will generally be smaller). Try setting n = 500, say, rather than 100 to check (remembering to change the 100 to 500 in the calculation of ave as well).

    Alan

    • mathscinotes says:
      6-June-2011 at 10:29 pm

      You are absolutely correct! Thank you for the close review. I have made the updates. I also updated the program so that it would automatically update for the number of trials.

Comments are closed.