Introduction
Figure 1: Example of Low-Landscape Lighting.
I have a beautiful new decking thanks to the guys at Composite Decking Boards | WPC Plastic Decking | UK Supplier and my backyard is looking better than ever, but it's not quite finished. I want some lighting out there and I have a small low-voltage lighting project in mind, similar to what shows in Figure 1 - though I did consider going for a Lampadaire exterieur, or outdoor lamp post first, after seeing them in people's gardens I'm fond of the low-level light the ones in Figure 1 show. I think they look so minimalist yet effective. I have not done a significant low-voltage wiring project in quite a few years, so I decided to do a bit of reading. It's quite a big project for a beginner so I wanted to do plenty of research to ensure I didn't make any mistakes. This comprehensive buyer's guide helped me learn more about which lighting to get and I've also watched lots of YouTube videos so that I can learn about installation. In one of the light vendor's manuals, I saw a table of allowed wattages for lighting as a function of distance and wire diameter. I thought it would be a useful exercise for me to duplicate the results shown in this table to confirm that I understand how the wiring works. This provides me some empirical verification that my "code" is correct.
While this is just a simple application of Ohm's law, it does a nice job of illustrating how to use a computer algebra system (Mathcad) to solve this type of problem. It also illustrates how even simple problems involve assumptions and approximations.
Many low-voltage wiring installation manuals include a table of allowed wattages as a function of wiring distances and wire gauge. I noticed that they are nearly all different. As I looked at the various tables, it appears that each table assumes a specific lamp layout (be it a photo moon lamp or other kind) – a layout that is often not named. I thought I would examine one of these tables in detail to see if I really understood what is going on. This post summarizes this analysis work.
Most of the installation manuals are still written assuming a halogen bulb. Outdoor LED fixtures are just starting to become common. While my work here will focus on the duplicating the results of a halogen bulb-based table, but it can easily be extended to be applicable for LED fixtures.
Background
Objective
The light level from a halogen bulb is strongly dependent on the voltage across the bulb and I want all the bulbs to have roughly the same level of brightness. Figure 2 illustrates the impact of voltage on light output (source). My design objective is to ensure that the voltages in the system are within 5% of each other, which means that light outputs should be within 80% of their nominal values.
Figure 2: % Luminous Output Versus % Design Voltage.
Load Assumptions
I needed to make a number of assumptions to create a simple model:
- These systems are referred to as "12 V", but the transformers that drive them often have taps for other voltages ? 12 V, 13 V, 14 V, 15 V taps are commonly seen. I will perform my analysis with the 13 V tap.
Most of the tables appear to use the 12 V tap, but the table I am working with here appeared to use the 14 V tap.
- All lamps are 12 V halogen.
There are LED lights available, but most of the design manuals are still targeted for halogen lights.
- The lamps are all equally spaced and we will model their load as a point load mid-way along the lamp run.
All the wiring tables I have seen appear to assume that the bulbs are arranged in a perfectly regular pattern.
- We are going to limit the amount of voltage variation between bulbs to 5% of the input voltage.
I have seen tables use voltage tolerance between 5% and 15%. The brightness of halogen bulbs is quite sensitive to the voltage applied to them – a 15% drop in voltage can result in a 50% reduction in light output (lumens).
Circuit Configuration
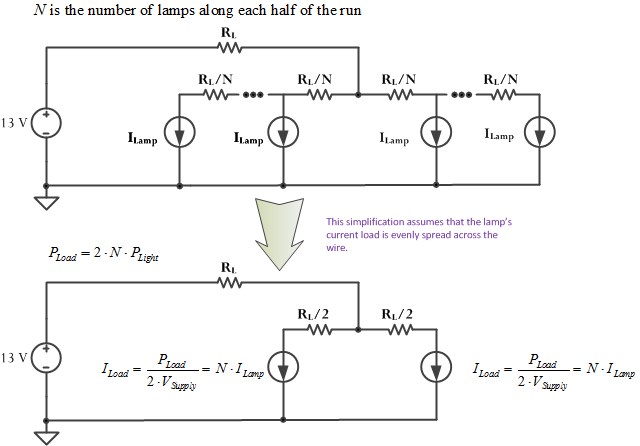
Figure 3 shows the schematic of the circuit that represents the low-voltage circuit discussed in the reference installation guide. I model the voltage drop for the distributed current load as if the all the current was sunk at the mid-point of the wire segment. I justify this approximation in Appendix A. You could also model it as half the total current was dissipated at the end of the wire segment.
Figure 3: Schematic of My Low-Voltage Lamp Circuit Model.
- The total length of the wire run of lamps is L feet, which has a resistance of RL ?.
This is a reasonable approach to designing this type of circuit.
- The power is fed into the center of the run of lamps.
This feed configuration reduces the voltage drop over driving the all the lamps in series.
- Each lamp is modeled as a current sink.
While a voltage-variable resistance would be more accurate, we are not going to allow the voltage across any lamp to be more than 5% different than any other point in the circuit. This means that the lamp resistance will not vary by much.
- The center of lamp run is fed by a wire of the same length as the total lamp run, which is 2L feet, which means there are L feet of lamps on either side of the center-feed.
You need to make some assumption as to how the voltage gets to the run of lamps.
Analysis
Reference Table
Figure 4 shows the reference table that I will be using for my design reference. It comes from this installation guide.
Figure 4: Reference Wiring Table.
Cable Resistance Versus American Wire Gauge
While I dislike using archaic units, all the wire at my local hardware store is sold with diameters specified in AWG and I have to use these units. I will proceed in two steps: (1) create a function to compute the resistivity of copper versus AWG, (2) model the resistance of copper wire using the copper resistivity function and its length and temperature.
Figure 5 shows my resistivity function. I have used this function for years and I forget where I got the data used in it. The units in it are atrocious - ?/m versus AWG. However, I have verified its correctness numerous times.
Figure 5: Copper Resistivity Versus AWG.
Figure 6 shows my cable resistance function with length, AWG, and temperature as input variables. The function includes the a table that describes how the resistivity of copper varies with temperature. The function is so old that I do not remember where I got this data, but I have used it in many applications before and it has been compared with other sources.
Figure 6: Mathcad Formula for the Resistance of Cable In Terms of Length, AWG, and Temperature.
Calculations
My model makes some simplifying assumptions:
- Wire power losses are small enough to be ignorable ? all power is lost in the bulbs.
- All bulbs use the same amount of power.
- The lamps are connected to the 13 V tap.
Figure 7 shows my calculations for duplicating the reference table (Figure 3).
Figure 7: My Version of the Reference Table.
This table contains very similar numbers to the reference table ? the differences are probably due to minor deviations between our models for the resistivity of copper.
Conclusion
I was able to duplicate the results in the reference table, so I think I understand how to determine the voltage drops in a simple low-voltage network. My layout will be different than this simple center-fed, single-run design. However, the design principles will be identical and I will use this model to ensure that my voltages are within my specifications.
Appendix A: Justification for Voltage Drop Approximation
Figure 8 shows how we can approximate the voltage drop across one lighting segment by assuming the total line current is sunk at the mid-point of the segment off the center-feed.
Figure 8: Justification for Use of Voltage Drop Approximation.