Wall-Wart Math

Posted on 7-June-2012 by mathscinotes

I have had some questions recently on the power conversion efficiency of AC power adapters (aka "wall warts"). I think my customers are becoming more concerned about energy costs. The questions that I received focused on how the efficiency of a wall wart varies with how heavily it is loaded (load factor = actual load/maximum rated load). For example, a wall wart rated for 20 W but driving a 1 W load would be considered lightly loaded (load factor = 1 W/20 W = 5%). The same 20 W wall wart with a 20 watt load (load factor = 20 W/ 20 W= 100%) would be considered heavily loaded.

I did a quick search of the web and I could not find any conversion efficiency data for standard wall warts. Fortunately the measurements are simple, however there is one interesting aspect -- the input current is very non-linear. This means that I must do a numerical integration of the instantaneous power (= input current times input voltage) to determine the average power. This actually is simple because multiplying signals and integrating them are built-in features of today's oscilloscopes. Figure 1 shows an oscilloscope screenshot of the wall wart input voltage, current, and power.

Figure 1: Oscilloscope Screenshot of Wallwart AC Input Voltage, Current, and Power.

Figure 1: Oscilloscope Screenshot of Wallwart AC Input Voltage, Current, and Power.

Figure 2 contains my graph of the efficiency versus load factor (load factor = actual load/rated maximum load). For comparison, I added a plot of the efficiency of a very common UPS to the plots for the wall warts.

Figure 2: Wall Wart Efficiency Versus Load Factor.

Figure 2: Wall Wart Efficiency Versus Load Factor.


The plots show that wall warts have relatively constant conversion efficiency when loaded at 30% or higher.

Note:
Here is a discussion of wall-wart power conversion efficiency by the NRDC folks.

Posted in Electronics | 2 Comments

Product Feature Presentations Using Excel's AutoFilter and VBA

Posted on 5-June-2012 by mathscinotes

I have to present a lot of data to people, but I find PowerPoint, a corporate workhorse, to be a poor vehicle for presenting data. I am not an acolyte of Tufte -- a famous PowerPoint critic -- I just don't like PowerPoint presentations. Recently, I had to prepare a presentation on the cost of various options for a product. I decided that I wanted to create selectable product scenarios that would create a dynamic bill of material using Excel's AutoFilter feature. AutoFilter is a really useful feature, but it does not allow me to predefine scenarios. Here is where a bit of Visual Basic for Applications (VBA) helped out. This spreadsheet was easy to present to a room full of staff, and it allowed our Marketing and Systems folks to try out product feature options themselves and to see just how much different features cost.

The basic idea is simple:

  • create a bill of material with parts assigned to specific features (on tab called AutoFilter).
  • create lists of scenarios consisting of feature sets that make sense (on tab called Definitions)
  • assign the scenarios to radio buttons.

Here is my source workbook: Scenario Presenter

Posted in Management | Comments Off on Product Feature Presentations Using Excel's AutoFilter and VBA

Computer Museum in Bozeman Montana

Posted on 25-May-2012 by mathscinotes

I am currently in Bozeman, Montana, and I just took a tour of the "Museum of Modern Human Progress," formerly known as the American Computer Museum. I was with one of my sons, and the museum provided us a great opportunity to view the history of information and computing. One interesting item that was not highlighted much is their copy of the Antikythera mechanism, which was an early Greek computer. I have always found that device and its history interesting.

It was nice seeing some of the old computer hardware I worked on as a "wee lad." However, it does make me feel a tad old.

Posted in History of Science and Technology | Tagged | 4 Comments

Square Law Potentiometer Circuit

Posted on 25-May-2012 by mathscinotes

Quote of the Day

The question isn't who is going to let me; it's who is going to stop me.

— Ayn Rand

I do not have an immediate need for a circuit that generates an output voltage proportional to the square of the potentiometer setting, but this circuit was interesting enough that I thought I would document it here. I found it while looking for a logarithmic potentiometer circuit.

Figure 1 shows the original article describing the circuit.

Figure 1: Circuit that Generates a Square Law Voltage Output Based on a Potentiometer Setting.

Figure 1: Circuit that Generates a Square Law Voltage Output Based on a Potentiometer Setting.

This circuit generates an output voltage given by V_{OUT} = {{k}^{2}} \cdot V_{CC}, where k is the potentiometer setting as a percentage of full scale and VCC is the supply voltage.

To explain how this circuit works, let's redraw the circuit using idealized components (Figure 2).

Figure 2: Idealized Representation of the Circuit of Figure 1

Figure 2: Idealized Representation of the Circuit of Figure 1

For {{V}_{CC}}=I\cdot {{R}_{P}}, this circuit generates a voltage output of {{v}_{OUT}}={{k}^{2}}\cdot {{V}_{CC}}. Figure 3 shows my derivation.

Figure 3: Derivation of Square Law Characteristic.

Figure 3: Derivation of Square Law Characteristic.

There are lots of ways to build a current source that are well documented on the web, so I won't go into detail here. I will attach a Maxim reference that I think is excellent.
AN3869

Empirical Results

Figure 4 shows a version of this circuit that I simulated using LT Spice (free simulator).

Figure 4: Square Law Circuit From Simulator.

Figure 4: Square Law Circuit From Simulator.

Figure 5 shows my empirical data. I did no resistor tuning. Just threw it together and it seemed to work well.

Figure 5: Empirical Results.

Figure 5: Empirical Results.

Save

Posted in Electronics | 5 Comments

Another Circuit with a "Logarithmic" Characteristic

Posted on 23-May-2012 by mathscinotes

Introduction

Electronics is my profession and my hobby (along with mathematics). For a hobbyist project of mine, I need an amplifier circuit with a programmable gain that varies exponentially with the setting on a potentiometer. When I design a circuit, I usually begin my design effort with a web search. I do not like reinventing the wheel. I found an old EDN article that has an interesting circuit, but the figures are not visible. I will reconstruct the circuit here based on the text description and make a small modification that makes it a bit more appropriate for my application.

Note that this problem is closely related to an early post of mine on potentiometers. I could use a log potentiometer, which really have an exponential resistance characteristic, but I have not been satisfied with the accuracy and repeatability of these components. So I have looked for an alternative approach and this one seems reasonable.

Requirements

I need a circuit with a gain that varies exponentially according to the setting of a potentiometer. Equation 1 shows the functional form that I am looking for.

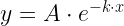Eq. 1 y=A\cdot {{e}^{-k\cdot x}}

where

  • x is the potentiometer setting as a percentage of full-scale.
  • k is an arbitrary constant.
  • A is an arbitrary constant.

I often end up plotting my results on a semi-log plot. Equation 1 represents a straight line on a semi-log plot, which I prove in Equation 2.

Eq. 2 \ln \left( y \right)=-k\cdot x+b\Rightarrow y={{e}^{-k\cdot x+b}}
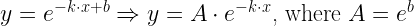y={{e}^{-k\cdot x+b}}\Rightarrow y=A\cdot {{e}^{-k\cdot x}}\text{, where }A={{e}^{b}}

Knowing that Equation 1 will plot as a straight line will allow us to graph the circuit response and determine how well it conforms to Equation 1.

Original Circuit

Because the schematic is no longer present in the article, I need to regenerate it. Figure 1 shows my guess for the schematic.

Figure 1: Schematic for a Circuit with Logarithmic Voltage Output.

Figure 1: Schematic for a Circuit with Logarithmic Voltage Output.

This circuit reminded me of some of the circuits my graduate school advisor, Arum Budak, used to come up with. A number of his circuits made clever use of op-amps driving potentiometer wipers. As he always did, I made sure sure that my opamps are "happy" -- which to Dr. Budak meant that the plus and minus inputs are at the same voltage (i.e. the virtual ground assumption holds). Another good aspect of the circuit is that both opamps are inverting. This follows the admonition of the great analog designer Jim Williams, who said "always invert (except when you can't)." Inversion is superior because the virtual ground eliminates common-mode errors.

Figure 2 shows that the gain of the circuit can be expressed as a function of the wiper setting as a percentage of the potentiometer's full scale setting.

Figure 2: Original Circuit Analysis.

Figure 2: Original Circuit Analysis.

Figure 3 shows the gain versus potentiometer setting (% of full scale) for the circuit of Figure 1. Note that the middle region of the curve is a straight-line, which indicates that Equation 1 holds in that region.

Figure 3: Voltage Gain Versus Potentiometer Setting for Circuit of Figure 1.

Figure 3: Voltage Gain Versus Potentiometer Setting for Circuit of Figure 1.

We see that this circuit has a linear gain characteristic on a semi-log plot in a range of x from 0.2 to 0.8. This is the circuit behavior is close to what I need and is good enough for me to proceed with.

While this circuit does generate an exponential gain curve, it is not very flexible. I only have one parameter that I can adjust, ß = R1/R3. This means that I can only adjust one aspect of the gain curve, say its slope or its value it a point. Ideally, I would like to adjust the gain curve's slope and set its value at a point. Let's see if we can make the circuit of Figure 1 just a bit more flexible.

Slightly Modified Circuit

The circuit of Figure 1 has a few shortcomings when it comes to implementing a specific exponential function:

  • There is only one parameter, the resistor ratio R1/R3.
  • The simplest thing for me to do would be to set the slope and value of my potentiometer circuit gain equal to the slope and value of my desired function at a point (e.g. mid-point of the range of x)
  • adjusting the slope and value of my potentiometer independently means that I need two independent parameters in my potentiometer circuit.

As I think about it, adding some fixed resistance on both sides of the potentiometer may be the answer. These resistors will give me another parameter to "tweak." Let's analyze the performance of the circuit of Figure 4.

Figure 4: Slightly Modified Circuit for Generation Ln(1/x).

Figure 4: Slightly Modified Circuit for Generation Ln(1/x).

Figure 5 shows my analysis of this circuit.

Figure 5: Analysis of My Modified Circuit.

Figure 5: Analysis of My Modified Circuit.

The circuit now has two parameters that will allow me to adjust the slope and circuit gain at a specific point. Let's work an example to illustrate the procedure.

Worked Example

Let's assume that we need a circuit with a gain described by the function 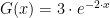G(x)=3\cdot {{e}^{-2\cdot x}}. My approach will be simple: (1) setup two equations in two unknowns, and (2) solve the resistor ratio ß = R1/R2 and the value of α = R0/RP.

  • create an equation for the slope of the potentiometer circuit at x=1/2 equal to slope of 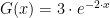G(x)=3\cdot {{e}^{-2\cdot x}} at x = 1/2.
  • set the gain of the potentiometer circuit at x = 1/2 equal to the value of 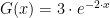G(x)=3\cdot {{e}^{-2\cdot x}} at x = 1/2.
  • solve these two equations simultaneously using the nonlinear solver in Mathcad.

Figure 6 illustrates how I used Mathcad's nonlinear solver to set my potentiometer circuit's parameters.

Figure 6: Nonlinear Solution for the Modified Potentiometer Circuit.

Figure 6: Nonlinear Solution for the Modified Potentiometer Circuit.

Figure 7 shows the level of agreement between my ideal equation and the potentiometer circuit output.

Figure 7: Gain versus Potentiometer Setting for the Modified Circuit.

Figure 7: Gain versus Potentiometer Setting for the Modified Circuit.

In my opinion, the result is pretty close. Good enough for the project I have going here.

Conclusion

This is a simple circuit that does what I need, which is to accurately render the exponential function over a limited range. I like the fact that I can obtain a dual opamp and linear potentiometer more readily than I can obtain an accurate and repeatable "logarithmic" potentiometer. See the Appendix for empirical Data.

Appendix

Figure 8 shows the circuit that I constructed in LT Spice.

Figure 8: Circuit in Spice.

Figure 8: Circuit in Spice.

Figure 9 shows a plot of the data from a quick test.

Figure 9: Circuit Test Results.

Figure 9: Circuit Test Results.

Save

Save

Posted in Electronics | Tagged | 7 Comments

High Definition Television Bandwidth and Compression Math

Posted on 15-May-2012 by mathscinotes

Quote of the Day

What is the difference between an introverted and extroverted mathematician? An introverted mathematician stares at his shoes when you are talking to him. An extroverted mathematician stares at your shoes when you are talking to him.

— I heard this joke on the radio.

Introduction

Figure 1: HDTV Example. (Source)

Figure 1: HDTV Example. (Source)

I frequently hear people make comments about the data bandwidth required for HDTV on home data networks and the levels of compression used for HDTV broadcasts. I usually hear two numbers cited:

These numbers are important for engineers because data bandwidth drives the design of networks, and compression ratios drive image quality. I thought it might be useful to review the bandwidth requirements of HDTV and the level of compression involved. I looked around on the web for this data and I could not find the level of detail that I wanted -- I will put it here.

As part of my job, I actually encountered one person who regularly watches 14 simultaneous HDTV feeds. He is a stock trader who works out of his home. He was displaying stock data from multiple markets on multiple televisions. Think about it -- 14 · 20 Mbps = 280 Mbps of television being watched by one person.

Background

What is a Pixel?

A pixel is the smallest addressable unit on a video display. Figure 2 (Source) illustrates how each pixel is composed of three color-generating components, called sub-pixels. At the display, each pixel is commanded to generate a combination of different red (R), green (G), and blue (B) color intensities.

Figure 1: Pixel Configuration on an LED HDTV.

Figure 2: Pixel Configuration on an LED HDTV.

Figure 3 illustrates how the different color intensities can be used to make different colors.

Figure 2: Examples of Color Generation Using Pixels.

Figure 3: Examples of Color Generation Using Pixels.

Figure 4 shows how a simple color image is formed by varying the pixel color mixture.

Figure 3: Close-Up Image of Microsoft Flag showing Pixel Settings.

Figure 4: Close-Up Image of Microsoft Flag showing Pixel Settings.

What are Luma and Chroma?

At the display, we need RGB intensities in order to drive the sub-pixels. It turns out that RGB is not the most bandwidth efficient way to transfer pixel information. It has been recognized since the early days of television that a more bandwidth efficient approach is to restate RGB in in terms of luma and chroma, which are defined as follows:

  • luma

    Luma represents the brightness in an image -- the black and white portion of an image. It expressed as a linear combination of the red, green, and blue components. Symbolically, luma is expressed as Y. It turns out the the eye is very sensitive to differences in luma. Television acknowledges the sensitivity of eye to luma by giving it preferred fidelity over chroma. Mathematically, luma is expressed (per Rec. 709) as

    \text{Y }=\text{ }0.\text{2126 R }+\text{ }0.\text{7152 G }+\text{ }0.0\text{722 B}

    Luma also allows us to easily generate a signal for black and white-only televisions, which is important for supporting legacy television hardware.

  • chroma (sometimes called CbCr)

    Chroma represents the color portion of an image. It turns out that the eye does not have as fine a color resolution as it does to differences in light and darkness. HDTV, through a process referred to as chroma sub-sampling, reduces its bandwidth requirements by making pairs of pixels share chroma values.

    Chroma consists of two components.

    • Cb

      Sometimes called the "blue difference," it is a scaled and shifted version B − Y.

    • Cr

      Sometimes called the "red difference," it is a scaled and shifted version of R − Y.

In summary, the advantages of representing RGB in terms of luma and chroma are simple:

  • low-end, black and white only systems can easily display Y and ignore CbCr.
  • to reduce bandwidth requirements, we can broadcast a luma value for each pixel and we can share a CbCr value between pixels.

Display Characteristics

In North America, calling a televised image "HDTV" generally means that the image has the following characteristics:

  • an aspect ratio of 16 by 9.

    I must admit that I really do like HDTV's 16-to-9 aspect ratio over standard television's 4-to-3 aspect ratio. I am a big fan of old movies that were photographed in wide-screen formats like VistaVision and CinemaScope. HDTV makes watching these movies much more enjoyable. Unfortunately, more lines means more bandwidth.

  • interlaced scanning.

    North American standard definition television projects images at a 60 Hz rate. While the HDTV standard does support projecting a new image at 60 Hz, all the systems I know of reduce their bandwidth requirements by projecting the same image twice. This means that a new image is projected at a 30 Hz rate, which reduces the bandwidth required by half. This approach is referred to as 1080i/30.

  • the refresh rate is really 29.97 Hz

    In North America, we typically refer to 30 Hz and 60Hz refresh rates. These rates are only approximately correct. Historically, North American HDTV has used a frame rate of 29.97 Hz (=30 Hz/1.001, a number which would require an entire post to explain). In truth, our HDTV should be referred to as 1080p/29.97.

  • transmit 8 bits of luma and 8 bits of chroma (alternating between Cb and Cr) per pixel (Reference)

    Each pixel also requires 24 bits of color information: 8 bits of Cb , 8 bits of Cr, and 8 bits of Y. Luma and 1/2 the chroma information are passed with every pixel transferred. This means adjacent pixels must share a chroma value.

We can use this information to compute the total number of pixels using the method shown in Figure 5.

Figure 4: Calculation of the Total Number of HDTV Pixels.

Figure 5: Calculation of the Total Number of HDTV Pixels.

Analysis

HDTV Transmission Over a Wire Pair

Given the discussion above, we can calculate the HDTV bandwidth at the camera (i.e. wire-transfer) as shown in Figure 6.

Figure 5: Calculation Summary for HDTV Bandwidth Without Compression.

Figure 6: Calculation Summary for HDTV Bandwidth Without Compression.

So Figure 6 tells us that the raw bandwidth out of a camera is just about 1 Gbps.

HDTV Broadcasting

There is some basic information needed to understand how HDTV is broadcast. First, everything is packed into a 6 MHz bandwidth, which is the bandwidth of a standard North American television channel. Because some of that bandwidth is used for a pilot tone and for filter transition regions, only part of the 6 Mhz bandwidth can be used for data. The basic bandwidth allocation is illustrated in Figure 7.

Figure 6: Allocation of Image Bandwidth in a 6 MHz Channel.

Figure 7: Allocation of Image Bandwidth in a 6 MHz Channel.

Television standards state that the total bandwidth (i.e. information + pilot tone + transition regions) of the television channel is 11.5% greater than the information bandwidth. The 11.5% factor is usually called α. This number goes way back to the old NTSC standard.

Once we have all the pixel data, there is some overhead involved in packing the image data into the 8VSB transport protocol. This overhead is illustrated in Figure 8.

Figure 7: Data Frame Structure for HDTV Data.

Figure 8: Data Frame Structure for HDTV Data.

Figure 9 illustrates the actual calculation of the actual image bits available from a broadcast HDTV picture.

Figure 8: HDTV Broadcast Bit Rate Calculation.

Figure 9: HDTV Broadcast Bit Rate Calculation.

Compression Rates

Since we have the broadcast data rate (19.3 Mbps) and the raw data rate (994 Mbps), we can state that the actual compression ratio = 994 Mbps/19.3 Mpbs = 51.5 ≈ 50. So I think we have established where the 50-to-1 compression ratio comment comes from.

Conclusion

I was able to show the assumptions involved when people state that HDTV requires 19.3 Mbps of data bandwidth and it has a compression ratio of about 50. If you look carefully at the calculations, you can see that HDTV bandwidth will be increasing in the future as the color sampling resolution increases from 8-bits to 10-bits and the real refresh rate increases to 60 Hz.

Figure 10 shows a slide from a video presentation by Sarnoff Corporation that mentions the 19.3 Mbps BW.

Figure 10: Alternative Reference on 19.3 Mbps Rate for HDTV.

 

Posted in Electronics | 9 Comments

Great Electronic Computer History Talk

Posted on 5-May-2012 by mathscinotes

Quote of the Day

People who claim that they're evil are usually no worse than the rest of us... It's people who claim that they're good, or any way better than the rest of us, that you have to be wary of.

— Gregory Maguire.

Figure 1: George Dyson. (Source)

Figure 1: George Dyson, historian. (Source)

I just watched a great lecture by George Dyson on the early days  (WWII era) of computer development and some of you may be interested in this topic as well. Dyson shares many stories about the legendary names in computer science: von Neumann, Turing, Eckert, etc. Dyson also had a special guest speaker at his lecture, Akrevoe Emmanouilides, who was a secretary working on the team developing MANIAC, an early computer. She is great!

Dyson Lecture on Early Electronic Computer History

Save

Posted in Electronics | Comments Off on Great Electronic Computer History Talk

Interesting Ratiometric Temperature Measurement Approach

Posted on 4-May-2012 by mathscinotes

Quote of the Day

Vitality shows in not only the ability to persist but the ability to start over.

— F. Scott Fitzgerald. It is very important to know when a task requires a "do over".

Introduction

Figure 1: The Lowly Thermistor. (Source)

Figure 1: The Lowly Thermistor. (Source)

As you can tell, I enjoy interfacing to sensors. Today, I was reading the usual assortment of engineering trade journals when I came across an interesting part from Lapis Semiconductor that is worth discussing here. It uses simple digital technology to make accurate resistor measurements. If you have a resistive sensor, it may be a good way to go. This approach could be used by other hardware devices as well, but the Lapis part is tailored for this particular technique. My focus in this post is on using a thermistor (Figure 1) for a resistive temperature sensor, but the same approach can be used for all sorts of resistive sensors.

Approach Description

Figure 2 shows a block diagram of how the part connects to a resistive sensor.

Figure 1: Highly Simplified Block Diagram of the Lapis Resistor Measurement Approach (RT1 = conventional resistor, RS1 = sensor resistor).

Figure 2: Highly Simplified Block Diagram of the Lapis Resistor Measurement Approach.

Note how the resistive sensor (RS1 in Figure 1) and a conventional resistor (RT1 in Figure 1) are both connected to a capacitor (CS1 in Figure 1). As there are at least four measurement modes supported, I will simplify this discussion by describing only one measurement approach. This approach can be described as follows:

  • Set a time interval over which to make the sensor measurement.
  • Disable the output for the conventional resistor and charge the capacitor through the sensor. When charged to a given level, cease charging the capacitor and increment a counter.
  • Discharge the capacitor very quickly (through IN1 in Figure 1). We will assume the discharge is infinitely fast compared to the charge.
  • Repeat this process multiple times until you reach the end of your test time. Call the count value NSensor.
  • Repeat the process performed with the resistive sensor on the conventional resistor RT1. Count the number of charge cycles you performed during the test time interval and call the count value NResistor

We can do a little math once we have the two charge counts (NSensor and NResistor). Figure 3 shows how we can compute the resistance of the sensor.

Figure 2: Derivation of Sensor Resistance Equation.

Figure 3: Derivation of Sensor Resistance Equation.

I usually avoid frequency-based approaches that use capacitors because capacitance varies with temperature. In general, this variation is unpredictable and adds error to my temperature measurement. However, taking ratios of the count values eliminates the dependence on the actual capacitance value. As far as the resistance-to-sensor parameter conversion, we can use a lookup table to translate the sensor resistance into what the sensor is reading (e.g. temperature, pressure, stress, etc).

Conclusion

I really like simple ways of reading and processing sensor data. This is a pretty good approach.

Save

Save

Posted in Electronics | Tagged | 1 Comment

Pioneer Anomaly Resolution Chat

Posted on 3-May-2012 by mathscinotes

Quote of the Day

The only man, woman or child who wrote a simple declarative sentence with seven grammatical errors is dead.

— E. E. Cummings , commenting on the death of President Warren G. Harding, a man considered by many to be our least intelligent president.

Figure 1: Pioneer 10. (Source)

Figure 1: Pioneer 10. (Source)

The Planetary Society has a wonderful audio program called Planetary Radio. For those of you interested in the Pioneer Anomaly and a suggested resolution, listen to this program. All sorts of reasons have been proposed for the odd orbital behavior of the Pioneer spacecraft and this one seems pretty reasonable. As with most things electrical, the bad behavior can be traced to the batteries ...

Save

Posted in Astronomy | Comments Off on Pioneer Anomaly Resolution Chat

Randomly Choosing a Winner from a Weighted List with Excel

Posted on 28-April-2012 by mathscinotes

Quote of the Day

Fashion is architecture: it is a matter of proportions.

— Coco Chanel. I hold the same view of product design. There is a balance that must be achieved between price, features, and schedule.

Figure 1: Dice Rolling Computer Style. (Source)

Figure 1: Randomly Choosing a Winner. (Source)

My wife is participating in a friendly contest at work that encourages employees to exercise. The employees record how many laps they walk around a set course during a month. At the end of the month, an Excel "drawing" is held to award a prize to one of the exercisers. To encourage more exercising, the likelihood of winning is to be proportional to the number of laps each person walked during the month. I was asked if I could write an Excel worksheet that would perform this task. I thought it was an interesting spreadsheet that was worth sharing here. There is a simple macro in the worksheet that controls when the worksheet re-calculates (otherwise it re-calculates a winner every time you change anything on the worksheet).

To make things simple for the users, the worksheet has the following features:

  • It uses a table that allows my wife to add people as new participants arrive with no change in the random chooser.
  • No "helper" columns are used, which are confusing to some folks.
  • The key calculation uses an array formula that generates a cumulative sum, which is a useful thing to have in your toolbox.
  • When you press the count button, it actually performs the randomizing six times. I wanted to make sure I avoided any random number start-up issues.

Random Chooser

Save

Save

Save

Posted in software | 42 Comments