How Much Does A Cloud Weigh?

Posted on 12-August-2011 by mathscinotes

Introduction

We have had a lot of rain in Minnesota this summer. As I sit here staring at the rain falling hard outside, I occurs to me that a cloud must be a very heavy thing in order to drop this much rain. It seems to me that figuring out the weight of a rain cloud would be a good Fermi problem. This cloud also dropped quite a bit of rain – how much of the cloud mass was lost as rain? Let's dig in …

Background

I need to round up some facts about clouds.

  • Clouds float for the same reason a balloon floats – cloud material weighs less than air.
  • The density of air at a typical altitude and temperature is about 1.007 kg/m3.
    This is an interesting number. Air is heavier than I thought. Think about it – a cubic meter of air weighs 1.0 kg, which is 2.2 lbs. For some reason that seems like a lot to me.
  • The density of cloud droplets is about 1.003 kg/m3.

Given these typical characteristics, lets try a specific example.

A Cloud Example

The cloud that hangs over my home can be modeled as a cuboid.

  • The cloud height (top to bottom) is 2 km (hCloud= 2 km)
  • The cloud length is 10 km (lCloud= 10 km)
  • The cloud width is 5 km (wCloud= 5 km)
  • This cloud dropped 2 inches of rain (lRain= 2 inches)

Analysis

A quick bit of Mathcad work gives me my estimate for cloud weight and the percentage of weight that rain represents.

Figure 1: Estimate of Cloud Weight and the Percentage Rain Represents of a Cloud.

Figure 1: Estimate of Cloud Weight and the Percentage Rain Represents of a Cloud.

Conclusion

I would have never guessed that a cloud weighed that much. I also am surprised that a major rainfall represents such a small portion of the weight.

Posted in General Science | 6 Comments

More Interview Criteria and A Funny Story

Posted on 3-August-2011 by mathscinotes

I read a management forum on LinkedIn that I like. The following exchange was on the forum yesterday that made me smile. Two people were discussing how to evaluate an interviewee.

Justin Hoffman • I use four simple guidelines (KSQB) Do they have the necessary industry "knowledge" to be successful. Do they have "skills" required for their role. Do they have the fundamental "qualities".

I can develop knowledge and skills over time but, I will never compromise on qualities. Qualities are many of the things noted above (integrity, leadership, drive, passion, honesty, etc.) I rank all candidates on a scale of 1-10. To this day I can go back and see a direct connection in candidates I have pushed or been pushed to hire that rank below an 8 on qualities. The net result is always the same...not good for either of us.

The last is a simple Y/N. Would I enjoy having a "beer" with this person after work. If I don't enjoy spending time with the people I work with then what's the point. I spend more time with my employees/co-workers than I do my own family. I better like them.

The response below is pretty funny. I have had the experience of finding a very qualified candidate that I would not necessarily want to spend a lot of hours with.

Dave Stevens • @ Justin, very good check list. I interviewed someone with an extensive and packed resume once, the font was below 6, but the sentence that stood out was her experience in the Alcohol Enforcement Patrol in law school, where she volunteered to snuff out all inappropriate drinking parties on their DRY campus. She was at the top of her class, a Jeopardy champion, and you could not touch her on accomplishments. But, the partners in this very large law firm thought she would conflict with our Friday scotch nights.

Posted in Management | 1 Comment

Capacitor Puzzle Redeux

Posted on 25-July-2011 by mathscinotes

My first blog post discussed the following interview question I received many years ago.

You are handed a 1 F capacitor charged to 10 V and two boxes containing uncharged capacitors: one box contains an uncharged 1 F capacitor and the other contains 1 million 1 µF capacitors. You can connect the capacitors from one box, one at a time, across the charged capacitor. Your job is to determine which box will allow you to discharge the voltage on the charged capacitor the most?

I received a comment recently from a reader who had looked at the problem and brought up an interesting aspect of the problem that I had not mentioned – energy does not appear to be conserved. My solution used charge conservation, so I skirted the energy conservation issue. Here is how the question came to me.

Meant to mention that these two problems together beg the question of how much energy is stored in the million charged 1uFs and, added to 6.7668 joules remaining on the 1F, how does the total compare to the original 50 joules. This is a tougher problem because each small cap is charged to a different – though calculable – value. I haven’t tackled that question yet; maybe you have.

Many problem solutions depend on some property remaining true throughout some transformation. A property that remain true throughout a transformation is called an invariant. There were clearly two candidate invariants in this problem: energy conservation and charge conservation. It turns out that the bookkeeping for the charge conservation is easier because this problem presents no opportunity to lose charge. Unfortunately, the bookkeeping for energy conservation is more difficult because energy can be lost in the interconnection between the capacitors. I will illustrate how using energy conservation for this problem presents an issue – how do I determine the losses that occur in the interconnection?

Let's begin my computing the energy on the 1 F capacitor before and after the million 1 microfarad capacitors have been attached. Since I am computationally lazy, I will write a Mathcad program to compute the result.

Figure 1: Energy on the 1 F capacitor before and after one million microfarad capacitors were attached.

Figure 1: Energy on the 1 F capacitor before and after one million microfarad capacitors were attached.


From this calculation we can see that the 1F capacitor loses about 43.2 Joules of energy. We now need to compute how much energy did the million one microfarad capacitors pick up, which is done below.
Figure 2: Energy on the One Million Microfarad Capacitors.

Figure 2: Energy on the One Million Microfarad Capacitors.


The million microfarad capacitors only ended up with 21.6 J of energy. Therefore, we are missing 42.3 J - 21.6 J = 21.7 J of energy.

Energy must be conserved, so where did the energy go? It was lost during the charge transfer through a combination of heat and electromagnetic radiation. This is why I used charge conservation for my invariant. I did not have a way to determine the energy loss that occurs during the connection.

Posted in Electronics | 4 Comments

Thermistor Mathematics

Posted on 22-July-2011 by mathscinotes

Quote of the Day

If Hitler invaded hell, I would have had a nice word or two for the devil in the House of Commons.

— Sir Winston Churchill, his response when asked why he was saying nice things about the Soviet Union after Hitler invaded the Soviet Union.

Introduction

Figure 1: Typical Thermistor Construction and Symbols (Source).

Figure 1: Typical Thermistor Construction and Symbols (Source).

A common electrical engineering task during the design of a circuit card is designing a way for the circuit to measure its own temperature. Knowing the temperature of a circuit board is important for compensating for component temperature variations and diagnosing heat problems. Normally, I use a thermistor as my temperature probe. A thermistor is a resistor whose resistance varies with temperature (Figure 1). The thermistors that I use have a negative temperature coefficient (NTC), which means their resistance reduces as their temperature increases. In many ways, thermistors are a great sensor: cheap, tough, small, and accurate.

Thermistors have one major drawback – their resistance variation with temperature is non-linear. Figure 2 shows how the resistance of a typical NTC thermistor varies with temperature.

Figure 1: Resistance Versus Temperature for a Murata NCP03XM102 05RL Thermistor.

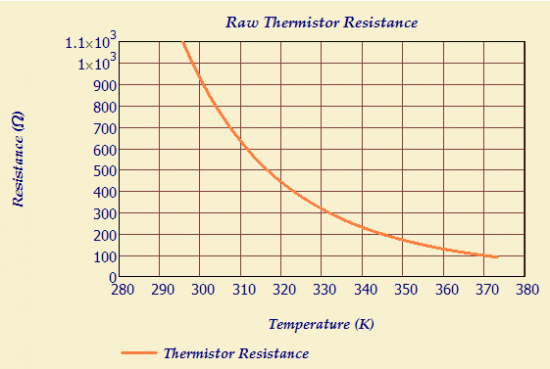
Figure 2: Resistance Versus Temperature for a Murata NCP03XM102 05RL Thermistor.

Linearity is a sensor characteristic that is loved by analog engineers. For this kind of problem, it means that calibration is simple (i.e. two points determine a line) and I do not need a processor around to implement complex compensation equations. The resistance characteristic of an NTC thermistor is too non-linear for my application directly. But what if I combined the NTC thermistor with other components in a manner that would somehow tame this non-linear response? This post will look at a common approach to linearizing the circuit response from a thermistor.

Problem Description

All engineering problems begin with determining requirements. Here is how I see my requirements for this problem:

  • Limited range of temperatures to be measured
    I only need to measure temperature over a limited temperature range (0 °C to 40 °C). This is considered the standard temperature range for indoor applications.
  • Minimal calibration
    Sensors usually require calibration, which is an expensive operation in production.
  • Generates a voltage that varies linearly (approximately) with temperature.
    I want a linear sensor to simplify my calibration. A linear sensor requires a couple of measurements to complete calibration.
  • Temperature accurate within 5 °C.
    This level of accuracy means that I can get by with an approximately linear sensor.
  • Minimal impact on software
    My processor is a very limited microprocessor (i.e. AVR) with minimal memory. I will use an analog-to-digital converter in the processor to read the voltage. I want the conversion from voltage to temperature to very simple. I have neither the memory nor time to require any fancy curve interpolation to get a simple temperature reading.
  • Minimal Printed Circuit Board (PCB) space because I only have space for a couple 0603-sized (i.e. 0.6 mm x 0.3 mm) components. Instead, you could consider contacting a PCB software specialist company for advice or help with this electrical engineering task (such as Altium for example).
  • Minimal cost
    I need something that costs pennies.
  • No integrated circuits.
    I am not wild about using an IC in this application. There are quite a few ICs that put out a voltage that is Proportional to Absolute Temperature (PTAT), but they generally require a power supply voltage that I do not have available or they cost too much.

Thermistor Characteristics

The resistance characteristic of Figure 1 can be modeled in a number of ways, but only two are really seen often: the Steinhart-Hart equation, and the ß-Parameter Equation.

The classic approach is the Steinhart-Hart equation (Equation 1). It is a very accurate model. In fact, it is far more accurate than I need.

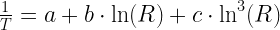Eq. 1 \frac{1}{T}=a+b\cdot \ln (R)+c\cdot {{\ln }^{3}}(R)

where

  • a, b, c are parameters that are chosen to fit the equation to the resistance characteristic.
  • R is the thermistor resistance (Ω).
  • T is the thermistor temperature (K)

While the Steinhart-Hart equation may be accurate, I have found it useless for use by an analog designer in a hardware application. It is simply too difficult to work mathematically without substantial software resources.

The ß-Parameter Equation is much more interesting to an analog engineer. Equation 2 shows the ß-Parameter Model as it is usually seen.

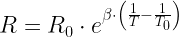Eq. 2 R={{R}_{0}}\cdot {{e}^{\beta \cdot \left( \frac{1}{T}-\frac{1}{{{T}_{0}}} \right)}}

where

  • R0 is the themistor resistance at temperature T0
  • ß is a curve fitting parameter.

The ß-Parameter Model is sufficiently accurate for my purposes and is much simpler to work with mathematically than the Steinhart-Hart equation. We will use this model for the remainder of this post.

Thermistor Linearization

Approach

Most thermistor linearization approaches involves adding parallel or series resistors. I will use a thermistor with a series resistor configured as a voltage divider (see Figure 3). This is the simplest linearization circuit that I can think of.

Figure 2: Simple Series Resistor Circuit for Thermistor Linearization.

Figure 3: Simple Series Resistor Circuit for Thermistor Linearization.

We will be measuring the output voltage (VOut) from the voltage divider, which is given by Equation 3.

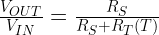Eq. 3 \frac{{{V}_{OUT}}}{{{V}_{IN}}}=\frac{{{R}_{S}}}{{{R}_{S}}+{{R}_{T}}\left( T \right)}

where

  • VIN is the voltage divider drive voltage.
  • VOUT is the voltage divider output voltage.
  • RS is the resistance of the series resistance.
  • RT(T) is the resistance of the thermistor.

To get an intuitive feel for the how the linearization occurs, you need to consider the asymptotic cases. For low temperatures, RT(T) is large relative to RS and the output is approximately 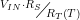{}^{{{V}_{IN}}\cdot {{R}_{S}}}\!\!\diagup\!\!{}_{{{R}_{T}}\left( T \right)}\;, which approaches 0 as the temperature drops. For high temperatures, RT(T) is small relative to RS and the output voltage approaches VIN. Figure 4 shows the thermistor resistance and the normalized output voltage versus temperature.

Figure 3: Example of a Thermistor's Resistance and the Linearized Voltage Divider Ratio.

Figure 4: Example of a Thermistor's Resistance and the Linearized Voltage Divider Ratio.

Look closely at Figure 4 and you will see an inflection point in the curve (452 Ω and 50 °C in Figure 4). At the inflection point, \frac{{{d}^{2}}}{d{{T}^{2}}}\left( \frac{{{V}_{OUT}}}{{{V}_{IN}}} \right)=0. After a long, tedious derivation (shown in the Appendix below), one can show that the inflection point can be moved where you want it by changing RS. Equation 4 shows the relationship between the temperature of the inflection point and the value of RS.

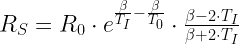Eq. 4 {{R}_{S}}={{R}_{0}}\cdot {{e}^{\frac{\beta }{{{T}_{I}}}-\frac{\beta }{{{T}_{0}}}}}\cdot \frac{\beta -2\cdot {{T}_{I}}}{\beta +2\cdot {{T}_{I}}}

where

  • TI is the temperature of inflection.
  • T0, R0 ,and ß are thermistor parameters given by the thermistor vendor.

The "rule of thumb" is to select RS to place the inflection point in the middle of your temperature range of operation. As you can see in Figure 4, this placement helps to minimize the maximum deviation from a line through the inflection point. However, it is not guaranteed to be the point of minimum error. When I need that level of accuracy, I use numerical methods to find the RS that minimizes the maximum error.

Example

Figure 5 shows a worked example of my thermistor calculations in Mathcad.

Figure 4: Example of Thermistor Calculations for Series Linearization.

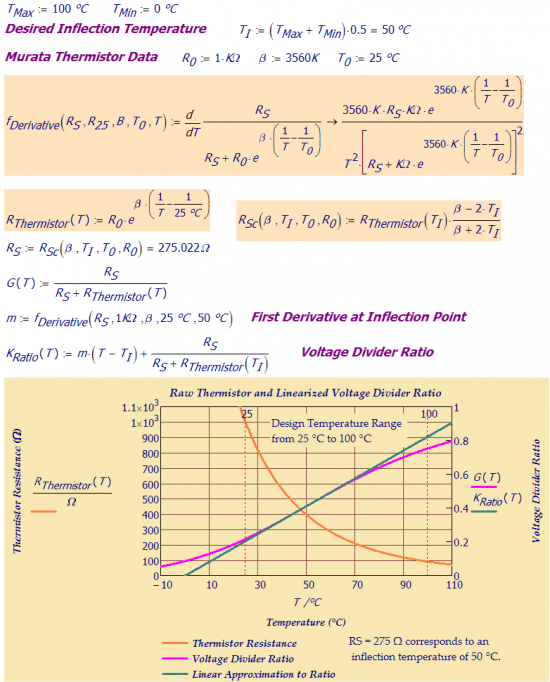
Figure 5: Example of Thermistor Calculations for Series Linearization.

Conclusion

The design of the linearization circuit for a thermistor is a nice use of basic calculus in an engineering application. Hopefully, some of you will find all the details presented useful.

Appendix

I wanted to record my derivation of Equation 4 so I would not have to go through the derivation pain again later, but since it is long and tedious I did not want to put readers through it – an Appendix seemed the appropriate place.

My approach is straightforward:

  • Develop an expression for VOUT using the ß-Parameter model.
  • Take the first and second derivatives of this expression.
  • Set the second derivative equal to zero.
  • Solve this expression for RS.

The derivation is shown in Equation 5. I will let the details stand for themselves.

Eq. 5 \text{Let }G\triangleq \frac{{{V}_{OUT}}}{{{V}_{IN}}}=\frac{{{R}_{S}}}{{{R}_{S}}+{{R}_{T}}\left( T \right)}
G=\frac{1}{1+\frac{{{R}_{{{T}_{R}}}}}{{{R}_{S}}}\cdot {{e}^{\frac{\beta }{T}}}}=\frac{1}{1+k\cdot f(T)}
\text{where }k\triangleq \frac{{{R}_{{{T}_{R}}}}}{{{R}_{S}}}\text{ and }f(T)\triangleq {{e}^{\frac{\beta }{T}}}
\frac{dG}{dT}=-\frac{k\cdot {f}'\left( T \right)}{{{\left( 1+k\cdot f\left( T \right) \right)}^{2}}}
\frac{{{d}^{2}}G}{d{{T}^{2}}}=-\frac{k\cdot {{f}'}'\left( T \right)\cdot {{\left( 1+k\cdot f\left( T \right) \right)}^{2}}-2\cdot \left( 1+k\cdot f\left( T \right) \right)\cdot {{k}^{2}}\cdot {f}'{{\left( T \right)}^{2}}}{{{\left( 1+f\left( T \right) \right)}^{4}}}
{{f}'}'\left( {{T}_{I}} \right)\cdot \left( 1+k\cdot f\left( {{T}_{I}} \right) \right)-2\cdot k\cdot {f}'\left( {{T}_{I}} \right)=0
\text{where }{{T}_{I}}\text{= inflection temperature}
{{f}'}'\left( {{T}_{I}} \right)+k\cdot {{f}'}'\left( {{T}_{I}} \right)\cdot f({{T}_{I}})=2\cdot k\cdot {f}'{{\left( {{T}_{I}} \right)}^{2}}
k=\frac{{{f}'}'\left( {{T}_{I}} \right)}{2\cdot {f}'{{\left( {{T}_{I}} \right)}^{2}}-{{f}'}'\left( {{T}_{I}} \right)\cdot f({{T}_{I}})}
k=\frac{\left( \frac{{{\beta }^{2}}}{T_{I}^{4}}+2\cdot \frac{\beta }{T_{I}^{3}} \right)\cdot f\left( {{T}_{I}} \right)}{2\cdot \frac{{{\beta }^{2}}}{T_{I}^{4}}f{{\left( {{T}_{I}} \right)}^{2}}-\left( \frac{{{\beta }^{2}}}{T_{I}^{4}}+2\cdot \frac{\beta }{T_{I}^{3}} \right)\cdot f{{\left( {{T}_{I}} \right)}^{2}}}=\frac{1}{f\left( {{T}_{I}} \right)}\cdot \frac{\beta +2\cdot {{T}_{I}}}{\beta -2\cdot {{T}_{I}}}
k\triangleq \frac{{{R}_{{{T}_{R}}}}}{{{R}_{S}}}=\frac{1}{f\left( {{T}_{I}} \right)}\cdot \frac{\beta +2\cdot {{T}_{I}}}{\beta -2\cdot {{T}_{I}}}\Rightarrow {{R}_{S}}={{R}_{0}}\cdot {{e}^{\frac{\beta }{{{T}_{I}}}-\frac{\beta }{{{T}_{0}}}}}\cdot \frac{\beta -2\cdot {{T}_{I}}}{\beta +2\cdot {{T}_{I}}}

You can also derive Equation 4 using Mathcad, which I demonstrate in Figure 6. The main issue with my Mathcad derivation is that many of the details are hidden. However, it took me less than a minute to complete it.

Figure 5: Mathcad Derivation of Equation X.

Figure 6: Mathcad Derivation of Equation 4.

Save

Save

Save

Posted in Electronics | 35 Comments

Speed of a Meteor

Posted on 8-July-2011 by mathscinotes

Quote of the Day

Failure is an option here. If things are not failing, you are not innovating enough.

— Elon Musk

Introduction

Figure 1: Meteor at Twilight.

Figure 1: Meteor at Twilight. (Source)

One of my coworkers knows one of my brothers (I have three). My brother and this coworker are friends and their families vacation together. They happened to be at a lake one night in Northern Minnesota together and my brother showed this coworker where to look for satellites and meteors. This coworker stopped by my desk and told me about the great time they had just watching the sky and how interesting it was.

I own a small cabin on a lake in Northern Minnesota. Years ago I showed my brother how to find satellites, planets, and meteors. I love to lay on the dock at night and watch the sky. Because Northern Minnesota is so sparsely populated, the sky is incredibly dark and the stars are so much brighter than in the metropolitan region where I spend most of my time. When people visit me at the cabin, I take them out on the dock and introduce them to the world of meteors, satellites, and planets. It is always a good time.

During a recent discussion on our sky-watching activities, a coworker mentioned that some meteor showers have "fast" meteors and some have "slow" meteors. Why are some meteors fast and others slow? What does fast mean? What does slow mean? This is another example of a Fermi problem and some simple mathematics will give us a feel for what the answer is.

Background

Meteor Shower Basics

I am not an expert on meteors, so I needed to do some research. It turns out there are three sources of meteors:

  • Asteroid belt
    The asteroid belt is the source of the slow-moving meteors, which are assumed to originate from collision between objects in the asteroid belt. The Geminides are a good example of this type of meteor shower.
  • Comets
    Comets have often been compared to "dirty snowballs" that orbit the Sun. They release rocky material as the heat of the Sun causes them to slowly disintegrate. Comets are the source of the fast-moving meteors. The Leonids are a good example of this type of meteor shower.
  • Outside of the Solar System
    These are very rare and unpredictable, so they would not be part of any well-known meteor shower. However, their velocity could be very high as they would not be in orbit of the Sun (by definition) and would be following hyperbolic trajectories. I will not be addressing this case here. However, one case has been discovered and it was moving very fast.

Computing Escape Velocity

All estimates of meteor velocity that I have seen involve a discussion of escape velocity. Escape velocity is the lowest velocity that a body must have in order to escape the gravitational attraction of a particular planet or other object.

We can compute the escape velocity by computing the work that a massive body does on a meteor. Equation 1 gives us the force on the meteor exerted by the gravity of an attracting body.

Eq. 1 {{F}_{Meteor}}=G\cdot \frac{{{M}_{Body}}\cdot {{m}_{Meteor}}}{{{r}^{2}}}

where

We can use Equation 1 to derive Equation 2, which is the work (i.e. energy) performed on the meteor by the gravitational field of the attracting body.

Eq. 2 {{E}_{Meteor}}=\int\limits_{\infty }^{{{R}_{Body}}}{-{{F}_{Meteor}}\left( r \right)}\cdot dr=G\cdot \frac{{{M}_{Body}}\cdot {{m}_{Meteor}}}{{{R}_{Body}}}

where

  • EMeteor is the work performed on the meteor by the attracting body.
  • RBody is the radius of the attracting body (I am assuming the attracting body is spherical).

Equation 3 equates the kinetic energy of the meteor with the work performed on the meteor by the attracting body.

Eq. 3 \frac{1}{2}\cdot {{m}_{Meteor}}\cdot v_{Meteor}^{2}=G\cdot \frac{{{M}_{Body}}\cdot {{m}_{Meteor}}}{{{R}_{Body}}}\Rightarrow {{v}_{Meteor}}=\sqrt{2\cdot \frac{G\cdot {{M}_{Body}}}{{{R}_{Body}}}}

where vMeteor is the speed of the meteor. We will use Equation 3 to estimate the speed of the meteors entering our atmosphere.

Analysis

Asteroid-Based Meteor Shower

In this case, we assume that the meteor has somehow broken free of an asteroid with negligible velocity and has simply fallen to the Earth. This means that its velocity at the surface of the Earth will be the escape velocity from the Earth. Figure 2 illustrates the calculation.

Figure 2: Illustration of Velocity for a Meteor Originating in the Asteroid Belt.

Figure 2: Illustration of Velocity for a Meteor Originating in the Asteroid Belt.

This calculation explains the 11 km/s speed sometimes quoted for slow meteors.

Comet-Based Meteor Shower

Comets orbit the Sun and the meteors generated by comets move at the velocity of a comet. These meteors really are orbiting the Sun and just happen to slam into the Earth. Figure 3 illustrates the calculation of their velocity.

Figure 3: Velocity of a Meteor Originating from a Comet.

Figure 3: Velocity of a Meteor Originating from a Comet.

This calculation explains the 42 km/s mentioned in the Wikipedia. The Wikipedia also mentions the peak velocity is 71 km/s, which is the speed of a comet-based meteor slamming heading on into an Earth that is moving at 29 km/s around the Sun.

Conclusion

I have seen the speed of meteors estimated to be anywhere from 11 km/s to 71 km/s. This post has shown where these numbers come from and they appear to be reasonable.

Save

Posted in Astronomy | 28 Comments

How to Interview Engineers

Posted on 29-June-2011 by mathscinotes

Quote of the Day

If something is important enough you should try, even if the probable outcome is failure.

- Elon Musk

Introduction

Figure 1: Team Interviewing.

Figure 1: Team Interviewing. (Source)

My youngest son has a long drive to and from work everyday. During his drive home, he frequently calls me to help him pass the time. During a recent drive, we talked about how I interview engineers, which I have done hundreds of times. I have a fairly standard interview methodology. The key part of any interview is how you go about grading the applicants.

In a previous post, I mentioned that I look for three things:

  • Pisstivity
  • Anality
  • Prima Donna Factor

My son was wondering what questions do I ask, and if they were anything like the challenging microsoft interview questions. Clearly, it was different from what he thought, and I explained it to him. He seemed to think the discussion was interesting and I thought it was worthwhile capturing some of it here.

Interview Process

I should go through my interview process quickly. From my point of view, there are three parts:

  • resume review
  • phone screen
  • in-person interview

I depend on the resume and phone screen to tell me if the candidate has the technical chops to work in my group. The resume gives me a feel for the candidates general work history. It also shows me how well they present information. An engineer must be able to write to work in my group. During the phone screen, I ask a lot of questions about things like their projects, the roles they played, and tools they have used (e.g. simulation, schematic capture, etc).

During the in-person interview, I really am looking at how well the person interacts with people. My basic approach is to start off with a few minutes of chit-chat to try to put the candidate at ease. After that, I try to find out what drives the person. I focus on questions like:

  • What project gave you the most satisfaction during your career?
  • Tell me about a project where you really made a difference technically?
  • What me about a project where you really made a difference non-technically (e.g. organizer, facilitator, mentor)?
  • Do you do anything technically in your spare time (e.g. astronomy, amateur radio, car stuff)

When I mentioned my questions, my son said that he has seen a good list of questions in a paper by a person named Buckingham that were similar to mine. Here are Buckingham's questions:

  1. What was the best day at work you've had in the last three months?
  2. What was the worst day at work you've had in the last three months?
  3. What was the best relationship with a manager you've ever had?
  4. What was the best praise or recognition you've ever received?
  5. When in your career do you think you were learning most?

Questions 1 and 2 give you an idea of the candidate's work values. Questions 3 and 4 tell you how a manager can motivate them. Question 5 tells you about their learning style.

Conclusion

I like Buckingham's questions and I have incorporated them into my basic set of interview questions. I am always looking for good interview questions. If any readers have questions they like to ask, please drop me a comment and tell me what you ask.

Posted in Management | 1 Comment

Another Analog Design Legend Dies

Posted on 20-June-2011 by mathscinotes

Quote of the Day

Politics is ethics done in public.

— Bernard Crick

Figure 1: Bob Pease, Analog Legend.Figure 1: Bob Pease, Analog Legend.

Figure 1: Bob Pease, Analog Legend. (Source)

I just saw the announcement that Bob Pease died in a car accident after leaving a memorial to Jim Williams, another analog legend. This is very sad. I have read everything that Bob Pease wrote. His column for Electronic Design, "Pease Porridge," was required reading for my crowd.

Jim Williams and Bob Pease were very important to the current generation of analog designers. They will be missed.

Posted in Electronics | Comments Off on Another Analog Design Legend Dies

Density of a Neutron Star

Posted on 19-June-2011 by mathscinotes

Quote of the Day

Some people get rich studying artificial intelligence. Me, I make money studying natural stupidity.

— Carl Icahn

Introduction

Figure 1: Example of Neutron Star System.

Figure 1: Example of Neutron Star System. (Source)

Television science programs frequently talk about black holes and neutron stars. A common quote during these programs is something like "a teaspoon of neutron star stuff weighs a billion tons" or some other similar statement. I always find numbers like these interesting to look at in detail.

Let's dig in  ...

 

Background

We are going to estimate the average density of a neutron stars, which means that we need to get some mass and volume information.

  • According to the Chandrasekhar limit, a neutron star must have a mass at least 1.44 times that of the Sun (mass of the Sun = 1 solar mass).
  • According to the Tolman-Oppenheimer-Volkoff limit, the upper limit on a neutron star's mass is between 2 and 3 solar masses. Collapsing stars more massive than the TOV limit form black holes instead of neutron stars.
  • The radius of a neutron star is between 10 and 15 km

My calculation is for the average density of neutron star stuff. Note that a neutron star does have structure and it is composed of material whose properties vary with distance from the core.

During my research, it became very clear that the physics of matter in neutron stars and black holes is still being worked out. As in every field, to really know a subject you must understand the corner cases and astronomers are still working this area out. Personally, I think its great because this means that there is more interesting science to come.

Analysis

Figure 2 shows the details of my analysis.

Figure 1: Estimate of Neutron Star Density.

Figure 2: Estimate of Neutron Star Density.

So my estimate is ~2 billion tons for a teaspoon of neutron star stuff. Since this is a Fermi-type problem, my estimate agrees with the statement of one billion tons per teaspoon.

How does the average density of a neutron star compare to the density of neutron? Figure 3 shows my estimate for the density of a neutron.

Figure 2: Estimate of a Neutron's Density.

Figure 3: Estimate of a Neutron's Density.

So the average density of a neutron and a neutron star are pretty much the same.

Conclusion

A neutron star does have a density of about a billion tons per teaspoon. Pretty incredible number when you think of it.

Save

Save

Save

Posted in Astronomy | Comments Off on Density of a Neutron Star

The Papoulis Filter (aka Optimum "L" Filter)

Posted on 17-June-2011 by mathscinotes

Quote of the Day

Two things prevent us from happiness; living in the past and observing others.

— Pinterest

Introduction

Figure 1: Athanasios Papoulis. (Source)

Figure 1: Athanasios Papoulis. (Source)

Analog engineers often have to design filters, which generally entails a lot of polynomial manipulation. Since I am currently designing some active filters, I thought it would be worthwhile documenting a filter function that I am using right now, but that is not widely known. This is the Papoulis or Optimum "L" filter. For this article, I will refer to this filter as the "L-filter." The "L" stands for Legendre, a mathematician whose like named polynomials are used in the derivation of the function.

This particular post made extensive use of Mathcad's symbolic processor. I left pretty impressed with what it could do.

 

Background

Most active filters are designed using one of four filter functions:

  • Butterworth
    This is a very friendly filter function. It has the flattest of all passbands and tends to have a well-behaved transient response because its poles are relatively low Q. Unfortunately, its roll-off rate is rather poor.
  • Chebyshev
    This filter is covered in every filter textbook, but I have actually never been able to use it. I have never been able to tolerate the ripple it creates in the passband. It does have very good roll-off characteristics.
  • Bessel
    I use this one a lot. The Bessel filter's linear phase characteristic gives it the best behaved transient response of all the filter functions, but its roll-off rate is very poor.
  • Cauer (Elliptic)
    I have used the Cauer filter quite a bit. It allows ripple in the stopband, which I usually can tolerate. It is a bit complicated to design and it has high-Q poles, which can create transient response problems.

These four filters have always been more popular than the L-filter. However, I certainly have had more use for the L-filter than for the Chebyshev. Since I was going through a design, I thought I would document it here.

History

The L-filter was developed by Athanasios Papoulis in a pair of articles published in 1958 and 1959:

  • odd-ordered polynomial: "Optimum Filters with Monotonic Response," Proc. IRE, 46, No. 3, March 1958, pp. 606-609
  • even-ordered polynomial:"On Monotonic Response Filters," Proc. IRE, 47, No. 2, Feb. 1959, 332-333 (correspondence section)

For a given filter order, the L-filter has the fastest roll-off rate of all filters with a monotonic magnitude response (i.e. the low-pass filter magnitude function always decreases with increasing frequency). I have used this filter a number of times in situations where I needed a relatively flat filter response and a sharp roll-off.

Comparison with Other Filter Functions

Figure 2 shows how the L-filter compares to the Butterworth and Chebyshev filters (all 3rd order in the figure).

Figure 1:Comparison of L-Filter, Butterworth, and Chebyshev Magnitude Characteristics.

Figure 2:Comparison of L-Filter, Butterworth, and Chebyshev Magnitude Characteristics.

Figure 3 shows how the L-filter characteristics change as the L-filter order increases.

Figure 2: Comparison of L-Filter Magnitude Characteristics for 3rd, 5th, and 7th Orders.

Figure 3: Comparison of L-Filter Magnitude Characteristics for 3rd, 5th, and 7th Orders.

Analysis

Function Definition

The definition of the L-filter function is rather complicated. Because I am mathematically lazy, I will be using Mathcad's symbolic processor to perform all the manipulations.

Legendre Polynomials

For detailed information on the Legendre polynomials, the Wikipedia is about as good as it gets. I chose to generate the polynomials using the recurrence relation shown in Equation 1.

Eq. 1 {{P}_{i}}\left( x \right)=1\quad i=0
{{P}_{i}}\left( x \right)=x\quad i=1
{{P}_{i}}\left( x \right)=\frac{\left( 2\cdot i-1 \right)\cdot x\cdot {{P}_{i-1}}\left( x \right)-\left( i-1 \right)\cdot {{P}_{i-2}}\left( x \right)}{i}\quad \text{otherwise}

n Odd

Equation 2 generates L(ω²) for filters of odd order.

Eq. 2 {{L}_{n}}\left( \omega _{n}^{2} \right)={{\int\limits_{-1}^{2\cdot {{\omega }_{n}}-1}{\left( \sum\limits_{i=0}^{k}{{{a}_{i}}\cdot {{P}_{i}}\left( x \right)} \right)}}^{2}}dx

where

  • Pi are the Legendre polynomials of the first kind.
  • ωn is the normalized frequency variable \left( {{\omega }_{n}}\triangleq \frac{\omega }{{{\omega }_{3\text{dB}}}},\text{ where }{{\omega }_{3\text{dB}}}=2\cdot \pi \cdot {{f}_{3\text{dB}}} \right)
  • f3dB is the 3 dB bandwidth of the filter.
  • \omega \triangleq 2\cdot \pi \cdot f,\text{ where }f\text{ is frequency}\text{.}
  • {{a}_{i}}\triangleq \frac{2\cdot i+1}{\sqrt{2}\cdot \left( k+1 \right)},\text{ where }k=\frac{n-1}{2}

n Even

Equation 3 generates L(ω²) for filters of even order.

Eq. 3 {{L}_{n}}\left( \omega _{n}^{2} \right)={{\int\limits_{-1}^{2\cdot {{\omega }_{n}}-1}{\left( x+1 \right)\cdot \left( \sum\limits_{i=0}^{k}{{{a}_{i}}\cdot {{P}_{i}}\left( x \right)} \right)}}^{2}}dx

where {{a}_{i}}\triangleq \frac{2\cdot i+1}{\sqrt{\left( k+1 \right)\cdot (k+2)}}, i\text{ even, 0 otherwise }\left( k=\frac{n-2}{2} \right).

Mathcad Routine for Determination of the L(ω²) function

Figure 4 shows the Mathcad routine that I developed to generate the Ln(ω²)(Equation 3).

Figure 3: Mathcad Routine for Determination of the L-Function.

Figure 4: Mathcad Routine for Determination of the L-Function.

Mathcad Routine for Determination of Filter Function

Figure 5 shows the Mathcad routine that I used to generate the actual filter function and my graphs.

Figure 4: Mathcad Routine for Generation of the Filter Function.

Figure 5: Mathcad Routine for Generation of the Filter Function.

L(ω2) Function

Table 1 shows the L(ω²) polynomials. Some folks have documented these polynomials instead of the characteristic polynomials. These polynomials are not directly useful for designs, but some web sites list them and they are useful for comparison purposes (i.e. verifying that my algorithm implementation is working correctly).

Table 1: L(ω²) Polynomials.
n L\left( {{\omega }^{2}} \right)
1 {{\omega }^{2}}
2 {{\omega }^{4}}
3 3\cdot {{\omega }^{6}}-3\cdot {{\omega }^{4}}+{{\omega }^{2}}
4 6\cdot {{\omega }^{8}}-8\cdot {{\omega }^{6}}+3\cdot {{\omega }^{4}}
5 20\cdot {{\omega }^{10}}-40\cdot {{\omega }^{8}}+28\cdot {{\omega }^{6}}-8\cdot {{\omega }^{4}}+{{\omega }^{2}}
6 50\cdot {{\omega }^{12}}-120\cdot {{\omega }^{10}}+105\cdot {{\omega }^{8}}-40\cdot {{\omega }^{6}}+6\cdot {{\omega }^{4}}
7 175\cdot {{\omega }^{14}}-525\cdot {{\omega }^{12}}+615\cdot {{\omega }^{10}}-355\cdot {{\omega }^{8}}+105\cdot {{\omega }^{6}}-15\cdot {{\omega }^{4}}+{{\omega }^{2}}
8 490\cdot {{\omega }^{16}}-1680\cdot {{\omega }^{14}}+2310\cdot {{\omega }^{12}}-1624\cdot {{\omega }^{10}}+615\cdot {{\omega }^{8}}-120\cdot {{\omega }^{6}}+10\cdot {{\omega }^{4}}
9 1764\cdot {{\omega }^{18}}-7056\cdot {{\omega }^{16}}+11704\cdot {{\omega }^{14}}-10416\cdot {{\omega }^{12}}+5376\cdot {{\omega }^{10}}-1624\cdot {{\omega }^{8}}+276\cdot {{\omega }^{6}}-24\cdot {{\omega }^{2}}+\cdot {{\omega }^{2}}
10 5292\cdot {{\omega }^{20}}-23520\cdot {{\omega }^{18}}+44100\cdot {{\omega }^{16}}-45360\cdot {{\omega }^{14}}+27860\cdot {{\omega }^{12}}-10416\cdot {{\omega }^{10}}+2310\cdot {{\omega }^{8}}-280\cdot {{\omega }^{6}}+15\cdot {{\omega }^{4}}

Filter Characteristic Function (s domain)

Table 2 shows the optimum L characteristic polynomials for n = 1 to 10.

Table 2: Optimum L Characteristic Polynomials.
n D\left( s \right)
1 \text{s+1}\text{.0}
2 {{s}^{2}}+1.4142 \cdot s+1
3 {{s}^{3}}+1.3107\cdot {{s}^{2}}+1.359039\cdot s+0.57736522
4 {{s}^{4}}+1.5628\cdot {{s}^{3}}+1.8878811\cdot {{s}^{2}}+1.2414681\cdot s+0.40821577
5 {{s}^{5}}+1.5515\cdot {{s}^{4}}+2.2034703\cdot {{s}^{3}}+1.692534\cdot {{s}^{2}}+0.89817083\cdot s+0.22356064
6 {{s}^{6}}+1.7262\cdot {{s}^{5}}+2.6898696\cdot {{s}^{4}}+2.4335933\cdot {{s}^{3}}+1.6332102\cdot {{s}^{2}}+0.67969552\cdot s+0.14143644
7 {{s}^{7}}+1.72772\cdot {{s}^{6}}+2.9926117\cdot {{s}^{5}}+2.9244072\cdot {{s}^{4}}+2.3320509\cdot {{s}^{3}}+1.2307095\cdot {{s}^{2}}+0.43791348\cdot s+0.075589885
8 {{s}^{8}}+1.86148\cdot {{s}^{7}}+3.4468776\cdot {{s}^{6}}+3.7236172\cdot {{s}^{5}}+3.3481719\cdot {{s}^{4}}+2.1192882\cdot {{s}^{3}}+0.99411199\cdot {{s}^{2}}+0.29972527\cdot s+0.045184527
9 {{s}^{9}}+1.8665\cdot {{s}^{8}}+3.7418201\cdot {{s}^{7}}+4.249464\cdot {{s}^{6}}+4.2481258\cdot {{s}^{5}}+3.0122773\cdot {{s}^{4}}+1.7075194\cdot {{s}^{3}}+0.68048233\cdot {{s}^{2}}+0.1815741
10 {{s}^{10}}+1.9744\cdot {{s}^{9}}+4.1713498\cdot {{s}^{8}}+5.0886545\cdot {{s}^{7}}+5.5135609\cdot {{s}^{6}}+4.3545176\cdot {{s}^{5}}+2.8312648\cdot {{s}^{4}}+1.3753686\cdot {{s}^{3}}+0.49627083\cdot {{s}^{2}}+0.11679607\cdot s+0.013743239

Factored D(s) for Single and Double Pole Realizations

When I design active filters, I usually implement them as quadratic and simple pole sections. This means the factored form of the denominator polynomial is easier for me to design with. Table 3 shows the factored form of the polynomials from Table 2.

Table 3: Factored Optimum-L Filter Polynomials.
n Factored D(s)
1 \text{s+1}\text{.0}
2 {{s}^{2}}+1.4142 \cdot s+1
3 \left( \text{s+0}\text{.6203} \right)\cdot \left( {{s}^{2}}+0.6904\cdot s+0.9308 \right)
4 \left( {{s}^{2}}+1.0994\cdot s+0.4308 \right)\cdot \left( {{s}^{2}}+0.4634\cdot s+0.9477 \right)
5 \left( \text{s+0}\text{.4681} \right)\cdot \left( {{s}^{2}}+0.7762\cdot s+0.4971 \right)\cdot \left( {{s}^{2}}+0.3072\cdot s+0.9608 \right)
6 \left( {{s}^{2}}+0.6180\cdot s+0.5830 \right)\cdot \left( {{s}^{2}}+0.8778\cdot s+0.2502 \right)\cdot \left( {{s}^{2}}+0.2304\cdot s+0.9696 \right)
7 \left( \text{s+0}\text{.3821} \right)\cdot \left( {{s}^{2}}+0.6984\cdot s+0.3060 \right)\cdot \left( {{s}^{2}}+0.4748\cdot s+0.6621 \right)\cdot \left( {{s}^{2}}+0.1724\cdot s+0.9765 \right)
8 \left( {{s}^{2}}+0.6006\cdot s+0.3829 \right)\cdot \left( {{s}^{2}}+0.3886\cdot s+0.7180 \right)\cdot \left( {{s}^{2}}+0.13788\cdot s+0.9809 \right)\cdot \left( {{s}^{2}}+0.7344\cdot s+0.1676 \right)
9 \left( \text{s+0}\text{.3257} \right)\left( {{s}^{2}}+0.3146\cdot s+0.7666 \right)\cdot \left( {{s}^{2}}+0.6188\cdot s+0.2090 \right)\cdot \left( {{s}^{2}}+0.4972\cdot s+0.4635 \right)\cdot \left( {{s}^{2}}+0.1102\cdot s+0.9845 \right)
10 \left( {{s}^{2}}+0.5548\cdot s+0.2702 \right)\left( {{s}^{2}}+0.0918\cdot s+0.9870 \right)\cdot \left( {{s}^{2}}+0.4284\cdot s+0.5282 \right)\cdot \left( {{s}^{2}}+0.2650\cdot s+0.8013 \right)\cdot \left( {{s}^{2}}+0.6344\cdot s+0.1218 \right)

Conclusion

My hope is that this post will help folks who find the need for another filter function option. I have found this function useful in a number of cases and maybe you will too.

Save

Save

Posted in Electronics | 13 Comments

The Passing of an Analog Electronics Giant

Posted on 14-June-2011 by mathscinotes

Quote of the Day

The difference between successful people and very successful people is that very successful people say 'no' to almost everything.

— Warren Buffet

Figure 1: Jim Williams, Analog Legend.

Figure 1: Jim Williams, Analog Legend. (Source)

I just saw the announcement that Jim Williams passed away. This guy was an inspiration to me. His apps work at National Semiconductor was a model for the industry. His articles in magazines like EDN provided real-world examples of elegant analog design techniques. His books, particularly Analog Circuit Design: Art, Science and Personalities, provided wonderful examples of problem solving. He will be missed.

I always smiled when I read his bio -- he had majored in psychology and did not have an engineering degree. I have worked with a number of self-taught engineers (Javi Sanchez is another). These folks are forces of nature. They are driven to design circuits.

One other thing -- photos of his desk always showed it to be messier than mine. That somehow always made me feel better about the clutter that I seem unable to avoid.

Posted in Electronics | Comments Off on The Passing of an Analog Electronics Giant