Parabolas and Avalanche Photodiodes

Posted on 6-January-2013 by mathscinotes

Quote of the Day

You have to perform at a consistently higher level than others. That's the mark of a true professional.

— Joe Paterno

Introduction

Figure 1: Typical Avalanche Photodidoe.

Figure 1: Typical Avalanche Photodiode. (Source)

During a meeting recently, a vendor was discussing the need for performing production calibration testing that required fitting a parabola to the data from an optical sensor called an Avalanche PhotoDiode (APD) (Figure 1). I recalled this comment while reviewing a test report this morning where I saw a parabola appear in an APD test report from an optical physicist in my group. I realized that our physicist and this vendor were working in related areas. It was an excellent test report that covered both the theoretical and experimental aspects of the subject. It also seemed like a good topic for this blog.

I thought this was a good example of a common situation in electronics:

  • You need to determine a physical parameter (e.g. average optical power) that is a function of some electrical parameter (e.g. voltage across a resistor).
  • The parameter is a nonlinear function of the electrical parameter -- in this case, the nonlinear function is a parabola.
  • Each component will have a slightly different nonlinear function that must be determined during the production testing for each part.
  • You want to minimize the amount of production data you must gather because the cost of gathering data increases with the amount of data.

This post will provide a brief description of how an APD is used in a optical receiver circuit and how we can measure the average optical power received by the APD.

Background

Optical Networks

My group builds Optical Network Units for GPON systems. The ONUs are mounted on the sides of homes and they contain both optical transmitters (i.e. lasers) and receivers (i.e. APDs). The APDs detect the light pulses on the fiber that convey information to the home. APDs are capable of detecting very small changes in light level -- in fact, they can even count individual photons when the used in the correct circuit. In this particular case, we want to measure average optical power and not instantaneous power.

The whole concept of using avalanche phenomena to create very sensitive detectors is an old one. APDs are very similar in concept to the Photomultiplier Tube (PMT). Geiger counters also use similar technology.

APD Background

For our work here, I am going to treat the APD as a mathematical object -- no circuit details. These details are not need to understand how we can measure average optical power using a photodiode. For our purposes here, there are three things we need to know about APDs:

  • They convert optical power into current.
  • The conversion factor between optical power and current is a function of the voltage applied to the APD.
  • The conversion factor is a highly nonlinear function of the voltage applied to the APD.

Equation 1 is the key equation showing the relationship between optical power and APD current.

Eq. 1 {{I}_{APD}}=M({{V}_{APD}})\cdot \mathscr{R} \cdot {{P}_{O}}

where

  • IAPD is the current through the APD.
  • VAPD is the voltage across the APD. This voltage is set during production to provide the desired level of amplification.
  • M(VAPD) is an adjustable gain (i.e. multiplication) factor. This is useful because we need to ensure that current from the APD is kept within the range of values that our electronics can measure.
  • \mathscr{R} is the responsivity of the photodiode. It is a conversion factor from optical power (Watts) into current (Amperes).

The multiplication factor, M(VAPD), is described by Miller's formula, which I state in Equation 2.

Eq. 2 M\left( {{V}_{APD}} \right)=\frac{1}{1-{{\left( \frac{{{V}_{APD}}}{{{V}_{B}}} \right)}^{n}}}

where

  • VB is the breakdown voltage of the APD. This is a critical parameter for all APDs.
  • n is a parameter that varies with the design of the specific device. We will assume n=1 for our work here.

During manufacturing, we adjust VAPD to achieve the desired gain. The setting of the gain is always a "Goldilock's Problem" -- the gain must be high-enough so that you can detect the minimum signal level you expect to encounter, but not so high that you saturate your detector with the maximum signal level you expect to encounter.

Current Mirror

The Wikipedia has a good working definition of a current mirror.

A current mirror is a circuit designed to copy a current through one active device by controlling the current in another active device of a circuit, keeping the output current constant regardless of loading.

In the case here, our current mirror actually makes a duplicate of 1/5 of the APD current. This scaling is useful because the APD current range is so wide that it is difficult to measure accurately without reducing its range.

Analysis

Schematic

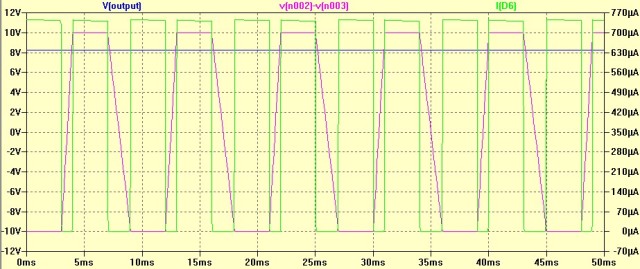
Figure 2 is a simplified schematic of the receiver circuit. The circuit here is based on one in a Maxim application note. There are different ways of implementing receivers, but this is a reasonable one.

Figure 1: Simplified Schematic of the Optical

Figure 2: Simplified Schematic of the Optical

Figure 2 deserves a few comments:

  • VOut is connected to the input of an A/D converter.

    The A/D converters have a limited range of voltages that they can convert. A typical range would be 0 V - 2.00 V. The current in the APD will increase as the APD receives more optical power.

  • CBypass is used to filter the APD current.

    For optical diagnostics, we are interested in the average optical power at the ONT. To measure the average optical power, we need to filter out the variations due to short-term variations about the average power due to changes in bit values (zero or one).

  • We measure the APD current by measuring the voltage across ROut.

    The use of the current mirror eliminates the need to make a direct measurement of the APD current.

Derivation of Optical Power Versus Output Voltage

After a bit of algebra, we can derive the parabolic relationship between optical power and VOut, which is shown in Equation 3. Observe that Equation 3 is a quadratic with no constant term.

Eq. 3 {{P}_{Optical}}=\frac{1}{{{K}_{A}}}\cdot \left( \frac{{{R}_{Sense}}}{\mathscr{R}\cdot R_{Out}^{2}\cdot {{V}_{B}}\cdot K_{M}^{2}}\cdot V_{Out}^{2}+\left( \frac{{{R}_{Out}}\cdot {{V}_{B}}}{\mathscr{R}\cdot R_{Out}^{2}\cdot {{V}_{B}}\cdot {{K}_{M}}}-\frac{{{R}_{Out}}\cdot {{V}_{App}}}{\mathscr{R}\cdot R_{Out}^{2}\cdot {{V}_{B}}\cdot {{K}_{M}}} \right)\cdot {{V}_{Out}} \right)

where

  • KM is the mirror current scaling. We are using 1/5 in this circuit.
  • KA is the relationship between the low-frequency component and total current values of the APD current. We will assume this value to be 1 in this case. In this application, the actual value is not important. It is a constant.
  • RSense is a the resistor we use to sense the APD current value.
  • VAPP is the supply voltage used to drive the APD bias voltage, which is constant.

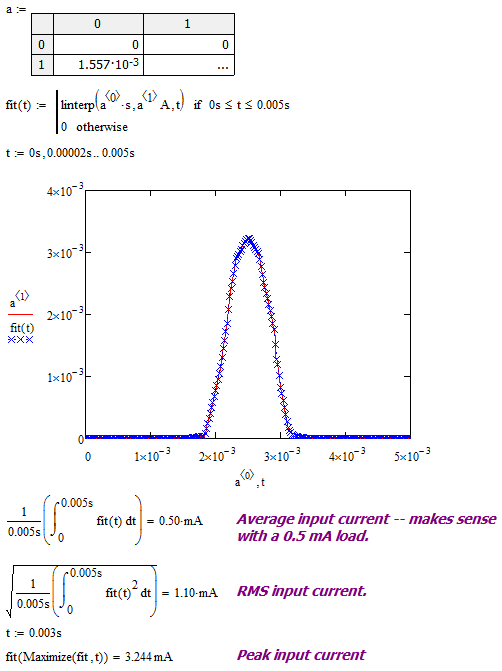
The details of the derivation are shown in Figure 3, which is a screenshot of a part of a Mathcad worksheet. Note that I did perform some minor algebraic manipulation of the Mathcad output to obtain Equation 3, which is a form that is a bit more useful to me.

Figure 2: Derivation of Optical Power Versus Output Voltage.

Figure 3: Derivation of Optical Power Versus Output Voltage.

Comparison with Empirical Results

In production, we will not be measuring all the individual parameters shown in Equation 3. Instead, we use the parabolic form derived above and determine the associated polynomial coefficients by fitting production calibration data to Equation 4. This approach is simpler and does not require gathering large amounts of data.

Eq. 4 {{P}_{Optical}}={{K}_{2}}\cdot V_{Out}^{2}+{{K}_{1}}\cdot {{V}_{Out}}

where

  • K2 and K1 are coefficients to be determined by curve fitting.

Observe how Equation 4 always passes through the origin. In actual use, we may choose to use a quadratic equation that includes a constant term (hence, three coefficients instead of two) because analog electronic parts always have DC offsets present that may be large enough that they must be compensated for.

Figure 4 shows how the empirical data compares to the parabolic model fitted to the data. The fit is very good.

Figure 3: Comparison of Empirical Data to Parabola Fitted to Data.

Figure 4: Comparison of Empirical Data to Parabola Fitted to Data.

In Figure 4, I used a large amount of data in the fitment process. In an actual manufacturing environment, every data point measured costs money. This model is for a parabola that passes through the origin. At a minimum, this means that only two more data points are needed to determine the required parabola. However, real measurements are always contaminated with noise and gathering additional data points can minimize the impact of this noise. There is a tradeoff that must be made between accuracy and cost.

Conclusion

This post shows a common sequence of mathematical modeling operations for an engineer:

  • Develop a formula template based on theory.
  • Perform lab experiments to verify the model.
  • Verify the data gathered fits the formula template that was developed.
  • Develop an efficient procedure for performing curve fitting in a production environment.

Save

Save

Save

Save

Save

Save

Save

Save

Save

Save

Save

Save

Posted in Electronics | Comments Off on Parabolas and Avalanche Photodiodes

Battery Failure Rates and Continuously-Compounded Interest

Posted on 2-January-2013 by mathscinotes

Quote of the Day

The man who does not read good books has no advantage over the man who cannot read them.

— Mark Twain

Introduction

7.2 A-hr Sealed Lead Acid Battery.

Figure 1: A Common Sealed Lead Acid Battery.

While performing some routine reliability analysis, I noticed that there is a similarity between battery aging and continuously-compounded interest calculations. I had not noticed this similarity before, and I thought I would document it here.

Figure 1 shows a common lead-acid battery. This chemistry is my focus in this post. Other chemistries will behave similarly, but the constants involved will differ. I will be assuming that the failure rate of the battery is described by the Arrhenius equation.

Background

To understand this post, we need to establish a bit of knowledge in two areas:

  • Chemical Reaction Rates and the Arrhenius Equation
  • Continuously Compounded Interest

Chemical Reaction Rates and the Arrhenius Equation

Batteries are chemical machines and their performance is predictable using the mathematics of chemical kinetics. For our purposes here, the key equation is the Arrhenius Equation, which I state in Equation 1.

Eq. 1 \displaystyle k=A\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot T}}}

where

  • A is a reaction-dependent constant.

    My work here will involve only relative values, which means that the exact value of A will not be important.

  • T is the absolute temperature.

    A common calculation error is to work in celsius and not Kelvin. Make sure that all your battery work is in Kelvin.

  • Ea is the activation energy.

    The primary corrosion reaction has an activation energy of about 50 kilo-Joules (kJ) per mole (reference).

  • R is the universal gas constant.

The Wikipedia has a very good article on the Arrhenius equation. I have also reviewed the Arrhenius equation in earlier post, and I will assume those in need of further review will venture there.

Continuously Compounded Interest

The Wikipedia provides some good background on continuously compounded interest. I will review the mathematics behind continuous compounding briefly here.

Equation 2 shows the basic compound interest formula.

Eq. 2 \displaystyle A=A_0 \cdot {{\left( 1+\frac{r}{n} \right)}^{n \cdot t}}

where

  • A is the final value of the investment (principal and interest)
  • A0 is the principal amount (initial investment)
  • r is the annual nominal interest rate
  • n is number of times the interest is compounded per year
  • t is number of years the investment receives interest payments

Assume that we want to compute the interest paid after one year (t = 1) to an account where the interest is compounded an infinite number of times (n = ?). Equation 3 shows the basic steps in the derivation.

Eq. 3 {{A}_{\infty }}=\underset{n\to \infty }{\mathop{\lim }}\,\ {{A}_{0}}\cdot {{\left( 1+\frac{r}{n} \right)}^{n\cdot t}}={{A}_{0}}\cdot {{e}^{r\cdot t}}

where

  • A? is the final value of the investment after infinitely many compounding cycles.

Assume we are interested in the amount of time required to double our investment assuming continuous compounding. Equation 4 illustrates that computation.

Eq. 4 \displaystyle 2\cdot A=A\cdot {{e}^{r\cdot t}}\Rightarrow t=\frac{\ln (2)}{r}

This equation is related to the famous "Rule of 72", which makes calculations of investment doubling time simple enough to do in your head (see here and here). It turns out that Equation 4 is also useful in computing the temperature increase required to halve the life of a battery.

Analysis

Battery Longevity's Relationship to Chemical Reaction Rates

The battery's longevity is determined by the speed of the corrosion reaction -- a faster corrosion reaction will corrode the battery faster and bring its demise sooner. No wonder why the concept of passivation is essential for metal. Not everyone is going to understand this topic in particular, but through companies such as astropak, you can learn even more about what the process of passivation involves. You learn something new everyday.
We can derive the impact of this faster corrosion reaction on the battery's lifetime by making a couple of assumptions:

    • The battery is considered failed when its capacity has been reduced below the level needed to provide adequate backup capacity.

      In the telcom industry, we normally consider a battery to have failed when its backup capacity is reduced to 80% of its initial value (see Telecordia's GR-909 for details)

    • Corrosion will gradually reduce the battery's capacity.

      The effects of corrosion are measurable in terms of battery impedance. UPS hardware usually incorporates some form of load test in order to determine if the battery's capacity has fallen a desired level.

Equation 5 shows that the battery lifetime will degrade exponentially with increasing temperature.

Eq. 5 D=\tau \cdot A\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot {{T}_{0}}}}}
{{D}_{0}}={{\tau }_{0}}\cdot A\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot {{T}_{0}}}}}
\tau =\frac{{{D}_{0}}}{A}\cdot {{e}^{\frac{{{E}_{a}}}{R\cdot T}}}={{\tau }_{0}}\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot {{T}_{0}}}}}\cdot {{e}^{\frac{{{E}_{a}}}{R\cdot T}}}
\tau ={{\tau }_{0}}\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot T\cdot {{T}_{0}}}\cdot \left( T-{{T}_{0}} \right)}}
\tau ={{\tau }_{0}}\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot T\cdot {{T}_{0}}}\cdot \Delta T}}

where

  • ? is the battery's lifetime at a temperature of T.
  • ?0 is the battery's lifetime at a temperature of T0.
  • T is the battery temperature for which we require an estimated lifetime.
  • ?T=T-T0.
  • D0 is the total amount of the corrosion chemical reaction required to degrade the battery to failure.
  • D is the total amount of the corrosion chemical reaction for a battery at a temperature of T for a time ?.

Unfortunately, Equation 5 contains two unknowns (i.e. ?T and T). We cannot directly solve Equation 5 without making an approximation. If we are only interested in temperatures near our reference temperature (T0), we can say that {{T}_{1}}\approx {{T}_{0}}\Rightarrow {{T}_{1}}\cdot {{T}_{0}}\approx T_{0}^{2} . Equation 6 gives us a useful approximation for the battery's lifetime at a temperature near the battery's reference temperature.

Eq. 6 \tau \approx {{\tau }_{0}}\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot T_{0}^{2}}\cdot \Delta T}}

Observe that Equation 6 is similar in form to Equation 3:

  • ?T in Equation 5 corresponds to t in Equation 3.
  • {{\tau }_{0}} in Equation 5 corresponds to A0 in Equation 3.
  • {{\tau }} in Equation 5 corresponds to A in Equation 3.
  • E_a / \left( R \cdot T0^2 \right) in Equation 5 corresponds to r in Equation 3.
  • ?T is the increase in temperature needed to halve the lifetime of the battery.

Given these correspondences, we can state that the temperature difference required to halve the battery lifetime is given by Equation 7, which is just Equation 3 with the listed substitutions.

Eq. 7 \frac{1}{2}\cdot {{\tau }_{0}}={{\tau }_{0}}\cdot {{e}^{-\frac{{{E}_{a}}}{R\cdot T_{_{0}}^{2}}\cdot \Delta T}}\Rightarrow \Delta T=\frac{\ln \left( 2 \right)}{\frac{{{E}_{a}}}{R\cdot T_{0}^{2}}}

Figure 2 provides an example for how the lifetime halving temperature for a typical lead-acid battery is computed.

Figure 1: Temperature Increase that Halves Battery Lifetime.

Figure 2: Temperature Increase that Halves Battery Lifetime.

The calculation in Figure 1 confirms that 10 °C value given here.

Conclusion

I found it interesting that a relationship I have used for years in financial analysis is also useful in battery life calculations. There is something almost magical about the way similar mathematics occurs in very diverse areas.

Save

Save

Posted in Batteries, Electronics | 1 Comment

Lead Acid Battery Life Math

Posted on 24-December-2012 by mathscinotes

Quote of the Day

The key to effective goal-setting is being realistic about what you can accomplish.

— Andrea Woroch

Introduction

7.2 A-hr Sealed Lead Acid Battery.

Figure 1: A Typical 7.2 A-hr Sealed Lead Acid Battery.

It is difficult to dig trenches for fiber optic cable in many parts of the US and Canada during the winter. Thus, winter is the time of year when telecommunications companies do their planning for fiber optic deployments during the following spring, summer, and fall. This planning time is when the service providers see the large amount of money they spend on replacing bad lead-acid batteries, and they start to ask what they can do to reduce the failure rates of these batteries. These inquiries are about as predictable as the arrival of Christmas. Today, I received a more detailed question than I usually do and I thought my answer was worth documenting for a wider audience.

Background

Battery Construction

Figure 2 shows a video that does a nice job showing how batteries are built.

Figure 2: Good Video Briefing on Battery Construction.

Battery Life Reduction With Increasing Temperature

Today, I was shown this specification and asked to explain how battery life can change so much with temperature. Figure 3 shows the battery life graph that was the focus of this discussion.

Figure 1: Battery Life Versus Temperature.

Figure 3: Battery Life Versus Temperature.

Figure 3 is a semi-log plot of the projected life of a 7.2 A-hr, Valve-Regulated Lead Acid (VRLA) battery versus temperature. Note that a range of battery lifetimes is given by this plot. This makes sense because battery lifetime will vary from unit-to-unit. Battery customers need to understand that battery life is not guaranteed -- you lifetime will vary based on the particular unit you have and how you treat it.

Failure Mechanism

Battery used in backup applications spend most of their lives at a float voltage. The main mechanism of failure in float applications is corrosion. Since I am not an electrochemist, I will simply quote a paper by a student of a battery expert:

The primary unavoidable aging effect is corrosion of the positive grid, composed initially of metallic PbO2, and is probably the most important factor for calendar life. This effect is also called grid growth because the electrode physically expands. [Wager] gives details on how the design of VRLA batteries can impact this fault mode, and on the chemistry of the process. In a nutshell, although we say that the positive electrode is composed of PbO2, this lead dioxide forms a dense corrosion layer around the metallic lead in the positive electrode when fully charged. This layer shrinks and expands during discharge and charge, and as it becomes fixed in a state of permanent corrosion, the grid is said to be corroded.

This quote is from this paper. Appendix A has a good infographic on how corrosion occurs.

While lead-acid batteries are simple at a high-level, there are many complexities when you start looking at the details of how they operate and eventually die. For a very good look at the details of battery chemistry, see this paper.

Analysis

Failure Analogies to Self-Discharge

VRLA batteries in backup applications maintain their batteries at a float voltage level, usually between 13.6 V and 14.4 V. You often see batteries described as having a life of 300-500 discharges. But what does this mean with respect to a backup power application where the battery is rarely discharged? Batteries in backup applications do fail, usually by damage caused by corrosion and not by charge/discharge cycles. This corrosion is a chemical reaction similar to the reactions that cause self-discharge, which I discuss at length here.

Standard Reliability Model

Equation 1 show the model used by most VRLA battery vendors. Unfortunately, the vendors use different values for T0 and T1, which means that you have to be careful about making direct comparisons.

Eq. 1 L={{L}_{0}}\cdot {{\left( \frac{1}{2} \right)}^{\frac{T-{{T}_{0}}}{{{T}_{1}}}}}

where

  • L_0 is the expected device lifetime at the reference temperature T_0.
  • T_0 is the temperature at which the device has lifetime L_0.
  • T_1 is the temperature increase required to halve the expected lifetime of the device.
  • T is the actual operating temperature. Note that few batteries spend their entire lives at a constant temperature. I will address the variable temperature case in a later post.

Equation 1 is actually an approximation based on the Arrhenius equation. I review the details of this approximation here.

Model Characteristics For Figure 2

Equation 1 can be used to generate the curve of Figure 1. The required parameters are:

  • L_0 = 10 years (the graph actually shows a small range -- this reflects the natural variability seen between units).
  • T_0 = 20 °C.
  • T_1 = 10 °C.

I did not need to do any analysis to make this determination. The battery is rated to have a nominal life of 10 years at 20 °C and you can see that the life halves every 10 °C. You can read these values right off of the graph.

IEEE Approach

Note that Figure 3 describes a situation slightly different than that presented by the IEEE (Figure 4). IEEE Standard 450-2002 for lead-calcium alloy VRLA batteries sets T0 = 77 °F and T1 = 15 °F. Minor differences between models like this are not surprising -- batteries are all built slightly differently, and these difference will affect their expected lifetime.

Figure 2: IEEE Thermal Degradation Curve for Lead Calcium Batteries.

Figure 4: IEEE Thermal Degradation Curve for Lead Calcium Batteries.

People always seem surprised that lower temperatures mean longer battery life -- it is true. However, the capacity of the battery is reduced over its nominal value (i.e. Amp-hr capacity @ 77 °C). This means that customers in cold climates may need to have larger battery packs (i.e. higher capacity) to provide the backup time they need under cold conditions.

Conclusion

This is just a quick note to document some of the material I went through today. I do have anecdotal evidence in support of Equation 1. Our customers in hot climates (i.e. Texas) that use outdoor batteries see relatively short lifetimes. We also have customers in cold climates (i.e. northern Minnesota) who have had good battery performance for long past their nominal ratings.

Appendix A: Good Battery Sludge Generation Infographic.

Figure 5 shows a good infographic on how battery sludge builds up in a battery (Source).

Figure M: Infographic on Battery Sludge Generation.

Figure 5: Infographic on Battery Sludge Generation.

Save

Save

Save

Posted in Batteries, Electronics | 2 Comments

Battery Charge Capacity and Energy Math

Posted on 16-December-2012 by mathscinotes

Introduction

I am doing some requirements analysis work on backup power systems for GPON ONTs. As part of this work, I need to perform an evaluation of a number of batteries for charge capacity and energy. As part of this evaluation, I decided to write a Mathcad worksheet to perform the analysis. When I write an analysis routine, I usually test it using some data that has already been acquired and processed. In this case, I grabbed some data from the web and used this data to test my worksheet. If you wish to look at the actual worksheet, you can download it here.

Background

I will be evaluating some lithium-ion batteries for charge capacity and energy as a function of the battery's discharge termination voltage (i.e. battery voltage at which discharge current is terminated). Not everyone is going to understand this topic in particular, but you can learn something new everyday such as the Avocet Battery Materials that go into lithium-ion batteries. However, the same approach can be used for any battery.

Reference Battery Data

I did some in depth analasys for my reference data on lithium-ion batteries and found some excellent data on this web site, which I will replicate here. The data is for a single-cell, lithium ion (LiCoO2) battery (type 18650). Like I mentioned before, there is a lot of excellent data on the web about this kind of battery.

Figure 1 shows data for this battery in the same format as I often receive from our lab when testing batteries. Basically, you use a current source to apply a fixed load on the battery. You then measure the variation in battery voltage versus time.

Figure 1: Battery Voltage Versus Discharge Current At Fixed Current Loads.

Figure 1: Battery Voltage Versus Discharge Current At Fixed Current Loads.

In addition to the raw test data, this web site also contains graphs of energy (Watt-hours) and charge capacity (amp-hours). Thus, I can compare my worksheet's results with those of the web site as check on my routine's correctness.

Analysis

Gather Battery Data

Using Figure 1 and Dagra, I converted the graph into numeric form. Figure 2 shows how this data appears in my Mathcad worksheet. Normally, I receive this data from the lab in the form of an Excel spreadsheet. Because I am looking for test data prior to doing my own tests, grabbing some test data from an exisiting graph is a good way to evaluate my Mathcad worksheet.

Figure 2: Captured Data in My Mathcad Worksheet.

Figure 2: Captured Data in My Mathcad Worksheet.

The arrays A, B, C, D, E, F each contain two columns of data (time and battery voltage) that corresponds to discharge currents 0.2 A, 0.5 A, 1.0 A, 2.0 A, 3.0 A, and 5.0 A, respectively.

Compute Battery Energy

The energy extracted from a battery as we draw current from it is given by Equation 1, which assumes the discharge begins with a battery charged to 4.2 V. As we draw energy from the battery, its terminal voltage decreases. Equation 1 will be used to generate a plot of energy drawn versus battery voltage.

Eq. 1 E\left( v \right)=\int\limits_{0}^{\tau }{{{v}_{Battery}}\left( t \right)\cdot {{i}_{Battery}}\left( t \right)}\cdot dt

where

  • E(v) is the energy drawn from the battery as the terminal voltage has dropped to v [Watt-hours].
  • vBattery(t) is the battery voltage [V].
  • iBattery(t) is the current being drawn from the battery [A].
  • is the time at which vBattery=v [hours].

Figure 3 shows the Mathcad formulas I used to compute the battery energy and a plot of the data generated from this analysis.

Figure 3: Calculation of Battery Energy.

Figure 3: Calculation of Battery Energy.

Compute Battery Capacity

The calculation of the battery capacity is a bit simpler than the calculation of battery energy. The formula I used is shown in Equation 2.

Eq. 2 \displaystyle Q(v)=\int\limits_{0}^{\tau }{{{i}_{Battery}}}\left( t \right)\cdot dt

where

  • Q(v) is the charge drawn from the battery as the terminal voltage has dropped to v [Ampere-Hours].

Figures 4 shows how the charge capacity calculation was setup. Note that while Equation 2 contains an integral, the use of a constant current source load means that we just need to compute the product of the current and time.

Figure 4: Formula Setup for Battery Capacity Calculation.

Figure 4: Formula Setup for Battery Capacity Calculation.

Figure 5 contains that graph of the charge capacity calculation results.

Figure 5: Capacity Calculation Results.

Figure 5: Capacity Calculation Results.

Conclusion

My worksheet generates very similar results to those posted on the reference web site. The only differences that I see between Figures 6 and 7 and the results my worksheet is generating are related to errors in grabbing the data off of the images -- there is always some error in that process.

At this point, I feel comfortable that my Mathcad routine is running properly and I can use this routine to process data being taken in my lab.

Figure 6: Vendor Measurements of Battery Capacity.

Figure 6: Vendor Measurements of Battery Capacity.

Figure 7: Vendor Data on Battery Energy.

Figure 7: Vendor Data on Battery Energy.

Posted in Batteries, Electronics | 4 Comments

Outdoor Enclosure Temperature Profile Math

Posted on 9-December-2012 by mathscinotes

Introduction

We build products that mount on the outside of homes -- homes that can be anywhere in the world. This means that the temperatures can be brutally cold (e.g. -46 °C in Bemidji, MN) or brutally hot (e.g. 49 °C in Death Valley, CA). Exposure to the Sun adds to these temperatures, which we call solar load. We have been having discussions with one of our vendors about the projected reliability of their parts. This particular part is very sensitive to the total amount of time it spends above a certain temperature. Since we design our equipment to operate reliably for least 10 years under worst-case conditions, it is important for us to determine how much time this part will spend above this threshold temperature.

After some discussion, we decided to use Phoenix as our climatic reference. It is a hot place with excellent climatic data. We also have product deployed in the area that will allow us to compare our temperature profile projections with actual data. Unfortunately, I need data now and I cannot wait a year to acquire the temperature data.

In many ways, I needed a "Fermi" type answer -- order of magnitude results would have been fine. I ended up doing extensive calculations because I had no intuitive feel for the situation. However, these calculations just took a couple of hours. Complex temperature simulations would have taken weeks. I view this approach a "middle of the road" course. After shipping out the work, the following quote came to mind.

If a thing is worth doing, it's worth doing well - unless doing it well takes so long that it isn't worth doing any more. Then you just do it 'good enough' --Programming Perl, Wall and Schwartz

Background

Here is the background on the reliability of the part we are investigating in this post:

  • The part is an integrated circuit

    There is an enormous amount of data that demonstrates that integrated circuit reliability is strongly related to temperature (link to a good reference).

  • Our vendor is stating that operation above 110 °C will result in degraded operational lifetime.

    You often see 110 °C listed as a maximum junction temperature guideline. I first encountered this limit while working on government contracts where Willis Willoughby advocated 110 °C as a junction temperature limit (link to an example).

  • The lifetime degradation is a function of the total amount of time the part will run at junction temperatures above 110 °C.

    The vendor knows their part and this is what they are telling us.

  • We are looking for an approximate answer.

    Climatic conditions vary widely throughout the year and from year-to-year. We are looking for a rough estimate of the average number of hours per year we could expect this part to operate above 110 °C.

Thermal modeling of a passively cooled enclosure is a complicated manner. We have Computational Fluid Dynamics (CFD) software that does a good job of predicting the temperatures in an enclosure, but it is time consuming to perform this type of analysis for all the days of the year. We are looking for an approximate approach. After some discussion, we decided to model our problem as follows.

  • We define the effective ambient temperature within the enclosure as the outside ambient temperature from the National Weather Service (NWS) plus the additional temperature rise within the enclosure provided by solar exposure.

    Standard air temperature reported by the NWS is a shade value. We have tested our enclosures under conditions of maximum solar exposure and we know that the effective ambient temperature of an enclosure under maximum solar load is 19 °C above the actual ambient temperature of the air.

  • Our CFD analysis has shown us that the part's junction temperature will exceed 110 °C when the enclosure's effective ambient temperature is above 50 °C.

    The junction temperature is 110 °C when the part's package is at 90 °C. The part's package is at 90°C when the internal ambient air temperature is at 70 °C. We know that the electronic's power dissipation raises the internal ambient of the part by ~20 °C. Thus, when the effective ambient temperature is above 50 °C, we probably have problem.

  • We will model the effective ambient temperature by assuming that
    • Model the daily temperature profile using the model given <here>.
    • Set the maximum and minimum temperatures equal to the average daily maximum and minimum temperatures listed here.
    • Assume that the solar load-based temperature rise is proportional to the level of solar insolation.
    • At maximum solar insolation, we will assume the effective ambient temperature is 19 °C above the actual air ambient temperature.
    • Assume one, two week heat wave where the ambient temperatures exceed the average temperature and peaks to 49 °C (120 °F) for a couple of days.

Analysis

Approach

What I am about to do will appall the thermal analysis folks because I am modeling a nonlinear problem completely linearly. Again, I need a rough answer quickly. Here is my approach:

  • Model the ambient air temperature.
  • Model the internal enclosure air temperature variation due to solar load
  • Sum the two models.
  • Compute the number of hours that exceed the threshold temperature of 50 °C

Ambient Temperature Modeling

A reasonably simple model of daily temperature variation is given here. Figure 1 shows a screenshot of my Mathcad implementation.

Figure 1: Model of Daily Temperature Variation.

Figure 1: Model of Daily Temperature Variation.

Solar Load Modeling

To estimate the solar insolation, I need to model how the amount of solar energy varies throughout the day. Fortunately, these models are readily available and I use this one.

insolation. The results of my CFD modeling shows that our enclosure's internal ambient temperature rises by 19 °C over the air ambient in Phoenix at maximum solar insolation. Figure 2 shows the screenshot of my Mathcad version of this model.

Figure 2: Model of Enclosure Temperature Rise due to Solar Load in Phoenix.

Figure 2: Model of Enclosure Temperature Rise due to Solar Load in Phoenix.

Combined Ambient Temperature and Solar Load Model

Figure 3 shows my combined ambient temperature and solar load model.

Figure 3: Combined Ambient Temperature and Solar Load Temperature Rise Model.

Figure 3: Combined Ambient Temperature and Solar Load Temperature Rise Model.

Summing Hours Enclosure Internal Ambient is Over 50 °C

Figure 4 shows my formulas for summing the hours over 50 °C during my model year.

Figure 4: Equations for Summing the Hours Greater Than a Threshold.

Figure 4: Equations for Summing the Hours Greater Than a Threshold.

Results

Figure 5 is the graphic that I generated to illustrate the number of hours that my enclosure's internal ambient exceeds 50 °C and other temperatures.

Figure 5: Projected Enclosure Internal Ambient Temperature Times.

Figure 5: Projected Enclosure Internal Ambient Temperature Times.

Conclusion

I am seeing that we will spend nearly 1000 hours per year above the 50 °C threshold temperature. This is more time than I would have expected. I will need to look at alternatives.

Posted in General Science | 6 Comments

Torpedo Data Computer Video

Posted on 9-December-2012 by mathscinotes

I am a fan of both naval history and the history of computing machines. I just saw a great video on the Torpedo Data Computer (TDC) that have I include here. The TDC was one of the last examples of an electromechanical analog computers. It played a major role in the Allied submarine war in the Pacific during World War 2.

If you wish more detailed information on the operation of the TDC, I have a number of posts on the topic. See these:

Some of you of a certain age may have seen analog computers in old science fiction movies. These films used analog computers as a kind of prop. The first analog computer I ever saw was a differential analyzer in When Worlds Collide. I am including a video here from Earth versus the Flying Saucers.

Not quite like the computer on Star Trek, but it did have nice penmanship.

Posted in Electronics, History of Science and Technology | 1 Comment

Network Cable Math

Posted on 6-December-2012 by mathscinotes

Introduction

Today I'm going to be discussing ethernet cables and if you've been reading this blog for a while, you know I'm no stranger to ethernet problems. I work with it quite a lot at work so I'm familiar with products like the ws-c2960s-48lps-l cisco catalyst and all the cables that ethernet entails. I am looking at category 5e (cat5e) cabling today. During some routine testing, I was seeing bit errors occurring on 100 meter long Ethernet cables that were operating at 60°C. This prompted me to investigate the effect of temperature on Ethernet bit error rate. Some businesses use a host server such as Hostiserver to minimise any faults and improve their web experiences. I found it surprising how complicated doing design work with these cables can be. In this post, I am going to review some basic cable characteristics and the kind of things that engineers need to look at when designing networks using these cables. There is nothing earth-shattering in this discussion -- things are just more complicated than you might expect. Let's dig in ...

Background

What Limits Cable Reach?

Most people think that the reach of Ethernet is 100 meters -- at true statement for a system operating at 20°C. We usually do not discuss what limits the reach of the cable. For the discussion at hand today, I will assume that signal attenuation limits the reach of the cable. There are other factors that can limit the reach of a system, but for today we will only look at signal attenuation.

The 100 meter reach number is based on some assumptions:

  • 90 meters of cat5e cable

    Cat5e cable is composed of 4 pairs of 24 American Wire Gauge (AWG) solid wires (8 wires total). The pairs are twisted to reduce the effects of electromagnetic interface. Unfortunately, the signal attenuates as it travels down the cable. The amount of attenuation is referred to as insertion loss.

  • 10 meters of cat5e patch cables

    Cat5e patch cables are composed of 4 pairs of 24 AWG stranded wires (8 wires total). The stranded wire is more flexible and is easier to bend than solid core wire, but it has higher insertion loss.

  • 4 connectors

    Connectors introduce additional losses that must be accounted for.

Communication systems are composed of transmitters, channels, and receivers. A minimum requirement for a reliable communication systems is for the transmitters to send a signal that is large enough for the receiver to clearly interpret after being attenuated by the channel.

Cat5e Attenuation Limits

The cat5e cable and connector attenuation limits are set by the industry standard TIA-EIA-568-B.2. I repeat these limits in Equation 1.

Eq. 1 \displaystyle I{{L}_{100mCable}}(f)\le 2.320\cdot \sqrt{f}+1.967\cdot f+0.050\cdot \frac{1}{\sqrt{f}}
\displaystyle I{{L}_{Connector}}\left( f \right)=0.040\cdot \sqrt{f}
\displaystyle I{{L}_{100mPatchCable}}\left( f \right)\le 1.2\cdot I{{L}_{100mCable}}(f)

where

  • IL100mCable is the insertion loss introduced by the 100 meters of cat5e cable (solid wire) at 20 °C.
  • IL100mPatchCable is the insertion loss introduced by the 100 meters of cat5e patch cable (stranded wire) at 20 °C.
  • ILConnector is the insertion loss introduced by a single connector at 20 °C.
  • f is the signal frequency expressed in MHz.

The industry has taken the approach that, as long as a cable has less attenuation than the specification's limit, enough signal from the transmitter will get through the channel to the receiver for reliable reception. Reliable reception is defined as a Bit Error Rate (BER) less than 1E-10.

Analysis

Insertion Loss @ 20 °C

Figure 1 shows a screenshot of the Mathcad worksheet that I am using for my analysis. I have duplicated the insertion loss chart of TIA/EIA-568-B.1.

Figure 1: 100 meter Cat5e Insertion Loss Calculation.

Figure 1: 100 meter Cat5e Insertion Loss Calculation.

Insertion Loss Increase at Higher Temperature

TIA-EIA-568-B-1 specifies how the insertion loss calculations are to be performed at elevated temperatures. Cable loss is to modeled as a 0.4% per °C increase in temperature. For the exact quote, see Appendix B. Since all the losses are multiplied by 0.4%/°C and we must keep the insertion loss under the 20 °C value at all frequencies, the maximum reach of Ethernet reduces by 0.4%/°C. So if we run our Ethernet over 60 °C cable, the maximum range is reduced by 16 meters. The calculation is shown in Equation 2.

Eq. 2 100\text{ meters }\cdot \left( 60\text{ }^\circ\text{C}-20\text{ }^\circ\text{C} \right)\cdot \frac{0.4\%}{^\circ\text{C}}= 16 \text{ meters }

Conclusion

It appears that the increased temperature I am encountering with this cabling is reducing the maximum length supported by Ethernet. I will need to adjust my test configurations.

Appendix A: Quote on Stranded Cable Insertion Loss Tax

The following quote from TIA-EIA-568-B-1 addresses the modeling approach to be used for cat5e patch cables.

Cat 5e stranded cable table shall meet the values computed by multiplying the horizontal cable insertion loss requirement in clause 4.3.4.7 by a factor of 1.2 (the de-rating factor), for all frequencies from 1 MHz to 100 MHz. The de-rating factor is to allow a 20% increase in insertion loss for stranded construction and design differences.

Appendix B: Quote on Cat5e Insertion Loss Increase with Temperature

The following quote from TIA-EIA-568-B-1 addresses the modeling approach to be used for cat5e patch cables.

Insertion loss is expressed in dB relative to the received signal level. Insertion loss shall be measured for all cable pairs in accordance with ASTM D4566 and 4.3.4.14 at 20 ± 3°C or corrected to a temperature of 20 °C using a 0.4%/°C correction factor for category 5e cables for the measured insertion loss.

Posted in Electronics | 7 Comments

Crest Factors for QAM Signals

Posted on 26-November-2012 by mathscinotes

Quote of the Day

If you want to succeed you should strike out on new paths, rather than travel the worn paths of accepted success.

— John D. Rockefeller

Introduction

I need to do a quick calculation of the Crest Factor (CF) for various types of Quadrature Amplitude Modulation (QAM) signals. CF is important to a hardware designer because higher CF values generally means more expensive components in order to meet the demand for high peak currents (or voltages) relative the the power delivered. As always, I first went to the Wikipedia to check out what they had on the subject. Unfortunately, the Wikipedia's article on CF only listed the QAM-64 CF (Note - I have since updated that Wikipedia page). Looks like I will need to compute the CFs for the other QAM options that I am interested in. I am sure they are in a reference somewhere, but I am short of time.

While performing this calculation, I decided to see if Mathcad's symbolic solver could give me a general equation for the CF of a QAM signal with a perfect square number of signal symbols (i.e. QAM-N2). It gave me a reasonable result that also produces a result for QAM-∞ that is the same as is listed in the Wikipedia.

Background

As far as information on QAM, Wikipedia's article on QAM is better than anything that I could write here.

The calculation on CF for a QAM signal is straightforward. Engineers normally discuss QAM signals in terms of a constellation diagram. Figure 1 shows a constellation diagram for QAM-16.

Figure 1: QAM-16 Constellation Diagram from Wikipedia.

Figure 1: QAM-16 Constellation Diagram from Wikipedia.

Crest Factor is defined as shown in Equation 1.

Eq. 1 \displaystyle CF=\frac{|x{{|}_{\text{peak}}}}{{{x}_{\text{rms}}}}

where

  • CF is the crest factor of the signal x (unitless)
  • xRMS is the RMS value of the signal x.
  • \displaystyle |x{{|}_{\text{peak}}} is the peak of the signal x.

CF can be computed for either currents or voltages. My focus here will be on voltages.

Analysis

Computational Approach

I need to compute the CF for QAM-4, QAM-16, QAM-64, and QAM-256. If I assume that all signals in the constellation are equally probable, the calculation is straightforward. Figure 2 shows my calculation in Mathcad. The numerator of my CF calculation is the maximum amplitude of the set of possible QAM signals. The denominator contains the RMS calculation for all the possible QAM signals assuming that they are equally likely. I also can ignore the absolute amplitudes of the various QAM signals because I am working with ratios.

Figure 2: Screenshot of my Mathcad Calculation of QAM Crest Factors.

Figure 2: Screenshot of my Mathcad Calculation of QAM Crest Factors.

These values make sense (i.e. agree with what I know to be true for QAM-4 and the Wikipedia entry for QAM-64). Figure 3 shows a plot of CF versus QAM constellation size.

Figure 3: Crest Factor Versus Constellation Size.

Figure 3: Crest Factor Versus Constellation Size.

Symbolic Analysis

I took the formula shown in Figure 2 and assumed a symbol number of N2, where N is an even number. Figure 4 shows the result of this symbolic analysis.

Figure 4: General Solution for Constellations with N<sup>2</sup> Symbols.

Figure 4: General Solution for Constellations with N2 Symbols.

Note that for constellations with a large number of symbols, the CF approaches \displaystyle \sqrt{3}.

Conclusion

Quick, simple calculation that solved my problem. I have added three appendices:

  • Appendix A that includes examples of square and non-square constellation configurations.
  • Appendix B shows one way of computing the crest factors for both square and non-square constellations.
  • Appendix C shows an excerpt from a reference that derives the same general equation as presented here.

Appendix A: Constellation Examples

Figure 5 shows some constellation examples. Note how the non-square constellations have their corners cutoff. Other configurations are possible and each will have different crest factors.

Figure 5:QAM Constellation Examples.

Figure 5:QAM Constellation Examples.

Appendix B: Crest Factor and PAR Calculation for Non-Square Constellations

Figure 6 shows an example of how I computed the crest factor and PAR for both square and non-square constellations. Calculations are more tedious for non-square constellations because of the need to manually cutoff the corner points.

Figure 6: Alternative Calculation that Handles Square and Non-Square Cases.

Figure 6: Alternative Calculation that Handles Square and Non-Square Cases.

These numbers agree with the table included in this here.

Appendix C: Reference that Discusses Crest Factor for Square Constellation Sizes

Figure 7 shows a reference that I found that presents a general formula for Peak-to-Average Power Ratio (PAPR), which equals CF2. The answers are the same as I present here.

Figure 7: Statement of General Solution for Square Constellations.

Figure 7: Statement of General Solution for Square Constellations.

Posted in Electronics | 22 Comments

Trapezoids Better Than Sinusoids?

Posted on 22-November-2012 by mathscinotes

Quote of the Day

The worst enemy of life, freedom and the common decencies is total anarchy; their second worst enemy is total efficiency.

— Aldous Huxley

Introduction

Figure 1: Trapezoidal Specification Example. (Source)

Figure 1: Trapezoidal Specification Example. (Source)

Sinusoids hold a revered place in electrical engineering -- they should. However, I do encounter quite a few trapezoids in telecom power systems. During a meeting the other day, I was asked "Why do we use trapezoidal waveforms for Alternating Current (AC) signals like ringer voltages and remote power systems." It was a good question. I have written about the trapezoidal waveform before, but I have never explained why the trapezoid is used so frequently.

As with most engineering tradeoffs, our constant quest for lower cost at a specified level of performance will drive the answer. Let's dig in ...

Background

Assumptions

To simplify this discussion, I will assume that we are evaluating the relative merits of two types of AC power system output waveforms, sinusoidal and trapezoidal. Figure 2 shows my simple model for a trapezoidal power system. The sinusoidal model is identical except for replacing the trapezoidal waveform with a sinusoidal waveform.

Figure 1: Trapezoidal Power System Model.

Figure 2: Trapezoidal Power System Model.

The choice of power source waveform will have an impact on the load power converter's cost. Because there are far more loads in telecom systems than sources, the total system cost is usually driven by the cost of the load hardware. Thus, it is important to choose a power source waveform that will reduce the cost of the load's power converter.

I am going to ignore any cost differences in generating trapezoids versus sinusoids. The Total Cost of Ownership (TCO) for the system is dominated by the large number of loads, so a bit more cost in the generator is more than made up by the lower cost of the loads.

Key Idea

The TCO for power conversion systems is driven by their installed cost, operating efficiency, and failure rate. Systems that have high peak currents relative to their RMS input currents have a higher TCO than systems with lower peak to RMS input current ratio. The ratio of peak to RMS current is called the Crest Factor (CF). While I will focus on the CF for currents here, similar statements can be made for voltages as well. I focus on the current CF here because it is larger than the voltage CF. Power systems with diodes in them tend to see high current peaks because of the exponential dependence of diode current on diode voltage.

I can give you a number of examples as to why high CF drives system cost:

  • Capacitor Reliability

    The reliability of aluminum electrolytic capacitors are reduced when they must support large ripple voltages. High CF tends to create high ripple voltages across these capacitors.

  • Conversion Efficiency

    Systems with high CF have relatively high peak currents, which also results in RMS currents that are significantly higher than the average current draw. High RMS currents increase resistive losses in teh system, making the overall conversion efficiency lower. The lower conversion efficiency increases the total cost of ownership of the system by driving up annual operating costs.

  • Power Dissipation

    Power dissipation increases the load's operating temperature, which results in lower reliability.

  • Component Cost

    The cost of many components, like diodes, is driven by the peak current they must handle.

Ideally, we want to choose the voltage waveform that will minimize the CF level. The trapezoidal waveform is easy to generate and reduces the CF level in the system.

Some Definitions

We need to provide some precise definitions of the following terms.

Crest Factor (CF)
The crest factor is a waveform metric that is calculated from the peak amplitude of the waveform divided by the RMS value of the waveform. Mathematically, we compute crest factor using CF=\frac{|f{{|}_{\text{peak}}}}{{{f}_{\text{rms}}}}, where f represents the waveform. We can compute CF for either current or voltage. In this note, I focus on currents.
Peak Current (I_{Peak})
Peak current is the maximum current at which the product must meet its requirements.
Peak Voltage (V_{Peak})
Peak voltage is the maximum voltage at which the product must meet its requirements.
Root-Mean-Square (RMS)
The RMS value of continuous-time parameter is the square root of the arithmetic mean of the square of the function that defines the continuous parameter. Mathematically, we compute the RMS value using {{f}_{\text{rms}}}=\underset{T\to \infty }{\mathop{\lim }}\,\sqrt{\frac{1}{T}\int_{0}^{T}{{{[f(t)]}^{2}}}dt}, where f(t) is the continuous-time parameter (usually voltage or current). The RMS value of a waveform is always greater than or equal to its average. The proof is here.

Analysis

Rectified Input Characteristics

Most telecom loads use some form of bridge rectifier at their power input. Figure 3 shows a typical example.

Figure 2: Rectified Output Voltage.

Figure 3: Rectified Output Voltage.

The rectification process causes the input current draw to appear in the form of spikes that occur when the input waveform is at its peak. The input spikes occur because the input only draws current when the input voltage is higher than the voltage on the output capacitor. I found a couple of nice illustrations of this action on this web site and I repeat them here in Figure 4.

Figure 4: Excellent Illustration of the Input Current Draw Characteristics of a Rectified Input
Illustration of the Input Current Draw Spikes Input Current Draw and it Effect on the Input Waveform.

Example Circuit

Rather than use mathematics to beat this problem to death, I thought I would just perform a simulation. I downloaded the free simulator LTspice and put in a simple example circuit. This circuit is completely made up just for use in this example, so do not send me email telling me that there are better components I could use.

Figure 5 shows the LTspice simulation for the case of a sinusoidal input (10 V amplitude at 100 Hz). The circuit has a 0.5 mA current source for its output load.

Figure 4: Simulation Schematic for a Sinusoidal Input Voltage.

Figure 5: Simulation Schematic for a Sinusoidal Input Voltage.

Figure 6 shows the LTspice simulation for the case of a trapezoidal input (10 V amplitude at 100 Hz). The circuit has a 0.5 mA current source for its output load.

Figure 5: Schematic Configured for a Trapezoidal Input Voltage.

Figure 6: Schematic Configured for a Trapezoidal Input Voltage.

Simulation Results

Figure 7 shows the simulation results for the sinusoidal test case. Notice that the input current peaks at ~3.3 mA even though the actual output current is only 0.5 mA.

Figure 6: Simulation of the Rectifier Circuit with a Sinusoidal Input.

Figure 7: Simulation of the Rectifier Circuit with a Sinusoidal Input.

Figure 8 shows the simulation results for the trapezoidal test case. Notice that the input current peaks at ~0.820 mA, which is much less than the 3.3 mA peak for the sinusoidal test case.

Figure 7: Simulation of the Rectifier Circuit with a Trapezoidal Input.

Figure 8: Simulation of the Rectifier Circuit with a Trapezoidal Input.

Conclusion

Table 1 summarizes the results from my simulation effort. The actual calculations are a tad boring, but I have captured them in Appendices A and B.

Table 1: Summary of Average, RMS, and Peak Current Values By Input Waveform
Waveform Type Average Input Current (mA) RMS Input Current (mA) Peak Input Current (mA) Crest Factor
Sinusoidal 0.500 1.105 3.244 2.936
Trapezoidal 0.500 0.575 0.743 1.293

We can see from Table 1 that the crest factor is much lower for a trapezoidal input signal than for a sinusoidal input signal. This means the the cost of component can be minimized and the overall reliability improved if we use a trapezoidal waveform for our AC voltage waveform.

Appendix A: Average, RMS, and Peak Current Values for the Sinusoidal Input Waveform.

Figure 9 shows an example of basic sine wave current calculations.

Figure 8: Screenshot of Mathcad Worksheet Calculations for Average, RMS, and Peak Input Current Using a Sinusoidal Input Waveform.

Figure 9: Screenshot of Mathcad Worksheet Calculations for Average, RMS, and Peak Input Current Using a Sinusoidal Input Waveform.

Appendix B: RMS and Peak Current Values for the Trapezoidal Input Waveform.

Figure 10 is similar to Figure 9, but for a trapezoidal waveform.

Figure 9: Screenshot of Mathcad Worksheet for RMS and Peak Current Using a Trapezodal Input Waveform.

Figure 10: Screenshot of Mathcad Worksheet for RMS and Peak Current Using a Trapezoidal Input Waveform.

Save

Save

Save

Save

Posted in Electronics | 7 Comments

Design Review of Four Transistor Current Source

Posted on 20-November-2012 by mathscinotes

One of the engineer's in my group asked if I had any information on how a four transistor current source works. I decided that to pull together a quick Mathcad worksheet. The Wikipedia refers to this current source configuration as a four-transistor improved current mirror. Figure 1 shows an image of this circuit from the Wikipedia.

Figure 1: Four-Transistor Improved Current Mirror (Source: Wikipedia).

Figure 1: Four-Transistor Improved Current Mirror (Source: Wikipedia).

I have attached a PDF version of the Mathcad worksheet and included a link to Mathcad 15 source in a zip file. There is a macro in it that just generates the table of contents.

Posted in Electronics | 3 Comments