The Cost of Minting Coins

Posted on 11-February-2016 by mathscinotes

Quote of the Day

I saw the angel in the marble and carved until I set him free.

— Michelangelo. I often feel that this is what a good manager does with a employee. The same is true is with good teacher or parent. We see something in a person and help them realize their potential.

Introduction

Figure 1: Some US Coins.

Figure 1: Some US Coins (Source).

I rarely think of the US government as producing any physical products, but there is one product that only it produces and that is extremely profitable – US money.  The government sells money at its face value, which historically has had higher value than the cost of manufacturing it. In the year 2010, the US Mint generated $6.3 billion in profit from selling the money it manufactures.

However, all is not well in world of coin minting. The penny and nickel now have production costs higher than their face value. This means that the government is now losing money on their production – $105 M in 2014. The US Mint is now considering eliminating production of the penny – an act that Canada has already taken with its penny. In this post, I will look at the cost of producing coins and see if I can understand the government's stated losses for penny's and nickels.

Analysis

All this post required was a bit of web scraping

Definition

When you talk about the government's sale of coins, you will often encounter the following word.

seigniorage
Profit made by a government by issuing currency, especially the difference between the face value of coins and their production costs.

Per Coin Cost/Lifetime

Table 1 shows the 2014 production costs for the most common coins.

Table 1: US Mint's Coin Production Costs.
Coin Cost (¢) Lifespan (months) Reference
Penny 1.8 300 Link
Nickle 9.4 300 Link
Dime 3.9 300 Link
Quarter 9 300 Link
Dollar Coin 12 360 Link
Dollar Bill 3 18 Link

The lifetime aspect of a coin versus a paper bill is very interesting. While the one dollar bill is cheap to make, it only lasts 18 months before you have to make a replacement. To keep one dollar in circulation for a 30 years costs the government 60¢ for a paper bill and only 12¢ for a coin – a paper bill cost 5x more than a coin to keep in circulation.  In other words, the dollar coin requires a higher initial outlay but a lower total cost of ownership.

Dollar coins have not been successful in the US. I regularly use them because the change machine in our company cafeteria puts them out when you insert a $5 bill.

Government Losses

I grabbed some coin production figures from the US mint web site, threw in the numbers I found for the cost of making the coins, and came pretty close to the government's stated 2014 loss of $105 M on penny and nickel production (Table 2). The government has net positive income from selling coins because the other coins (dimes, quarter, half-dollars, dollar) have positive seigniorage.

Table 2: Estimating the Government's Losses for Selling Penny's and Nickles.
Coin Penny Nickle
Face Value (¢) 1.0 5.0
Prod. Cost (¢) 1.8 9.4
Production Totals 8,146.4 M 1,206.2 M
Money Lost ($) $65.2 M $37.4 M
Total $102.6 M

Conclusion

I personally do not see much need for the penny. When I was a child, we actually did not use pennies often because most items were priced in terms of even numbers of nickels, dimes, and quarters. However, the imposition of a Minnesota sales tax in 1967 meant the now penny had a role in nearly every transaction. Now the government is considering getting rid of the penny because it is losing ~$100 M per year on making it – an amount less than the cost of one F35 fighter.

Posted in Financial | 2 Comments

MTBF and Annualized Failure Rates

Posted on 9-February-2016 by mathscinotes

Quote of the Day

If I had to give credit to the instruments and machines that won us the war in the Pacific, I would rate them in this order: submarines first, radar second, planes third, bulldozers fourth.

— Admiral Bull Halsey. I have always found the performance of US submarines during WW2 amazing considering the challenges that they faced with faulty torpedoes.

Introduction

Figure 1: Bathtub Curve Model of System Reliability.

Figure 1: Bathtub Curve Model of System Reliability. (Source)

One of the more distasteful tasks I need to do is make estimates of annual product failure rates using  MTBF predictions based on part count methods. I find this task distasteful because I have never seen any indication that MTBF predictions are correlated in any way with field failure rates. This is not solely my observation – the US Army has cancelled its use of part count method MTBF predictions (i.e.  based on MIL-HDBK-217). However, the telecommunications industry has continued to use these predictions through their use of Telcordia SR-332, which is similar to MIL-HDBK-217. If you want a simple example of an SR-332-based reliability prediction, see this very clear example from Avago. The parts count method assumes that components fail at a constant rate (green line in Figure 1).

While this calculation is simple, it is useful to discuss why the results generated are so useless – in fact, I would argue that they drive incorrect business decisions for things like required spare parts inventories.

Background

Theory

The basic math here is shown in Equation 1.

Eq. 1 \displaystyle {{\lambda }_{{Annualized}}}=\underbrace{\lambda }_{{=\frac{1}{{MTBF}}}}\cdot {{T}_{{Year}}}=\frac{{{{T}_{{Year}}}}}{{MTBF}}

where

  • λAnnualized is the failure rate per year.
  • λ is the failure rate (usually expressed per billion hours).
  • TYear is the number of hours in a year (8760)
  • MTBF is the Mean Time Between Failures.

Shortcomings

The shortcomings of the part count method are many:

  • It assumes a constant failure rate, memory-less failure rate
    • A new part fails at the same rate as an old one.
    • Total operating hours is all that is important.
    • This means 1000 parts operating for one hour fail is the same as one part operating for 1000 hours.
  • It assumes that a part's reliability is predictable based on some simple mathematical function.
    • I see wide variations in part failure rates that depend on the part's application and how the vendor build it.
    • I frequently see lot-dependent component failures.
  • Most part failures are not random.
    • They are caused by manufacturing issues, misapplication, environmental issues (e.g. lightning), etc.
    • In some cases, they are caused by wear-out (e.g. I just dealt with a rash of dried-out, ten-year old electrolytic capacitor failures)
  • It assumes that all vendors have the same quality level.
  • It assumes that system's failure rate is the sum of all the individual component failure rates.
    • Many issues are related to interaction problems.
    • Ignores the fact that how you hook up the parts matters.
  • Installation issues are a major source of equipment problems.
    • I frequently see installations where there is contamination or wind-generated motion that causes device failure.
    • I have reported on this blog numerous cases of insect infestation.
    • These issues drive field failure rates far more than random part failures.
  • The "elephant in the reliability room" is that software failures tend to dominate over hardware failures.

Analysis

Figure 2 shows my calculations for a made-up example.

Figure 2: Made-up Example Showing Annualized Failure Rate Calculation.

Figure 2: Made-up Example Showing Annualized Failure Rate Calculation.

Conclusion

In general, I find all formal procedures distasteful. In this case, people want a calculation done in a specific manner – and I dutifully comply. However, I know the answer does not reflect reality. In general, these computed annualized failure rates are ~10x what I would consider acceptable annual failure rates for actual products.

I recently had a conversation with an Australian service provider who was having trouble predicting the number of spare parts he needed to have in inventory. The problem he was having traced directly back to this calculation.

Save

Save

Save

Posted in Statistics | 8 Comments

Drag Coefficient From A Ballistic Drop Table

Posted on 8-February-2016 by mathscinotes

Quote of the Day

The Russians put our camera made by our German scientists and your film made by your German scientists into their satellite made by their German scientists.

— Jones in Ice Station Zebra

Introduction

Figure 1: Example Showing G7 Ballistic Characteristic Versus Actual Bullet.

Figure 1: Example Showing G7 Ballistic
Characteristic Versus Actual Bullet.

I thought it might be interesting show how you can approximate the drag coefficient for a bullet given a standard bullet velocity versus distance table. The folks at Barnes have put together a very nice discussion of how they go about characterizing a projectile using Doppler radar data. They also created an excellent infographic for a common hunting round showing the velocity versus distance table, actual drag coefficient, and G1/G7 reference drag coefficients (Figure 1). I thought I would take their table data and use that data to generate the drag coefficient chart. Since my data is limited, I do not expect a perfect reconstruction, but it should be close.

Background

General Drag Coefficient Information

I have discussed the drag coefficient in numerous other posts(e.g. here). For general drag coefficient background, it is hard to beat the Wikipedia article on the subject. The calculations are based on Equation 1.

Eq. 1 \displaystyle {{c}_{\text{d}}}=\frac{{2\cdot {{F}_{\text{d}}}}}{{{{\rho }_{{Air}}}\cdot {{v}^{2}}\cdot A}}

where

  • cd is the drag coefficient.
  • Fd is the drag force.
  • v is the projectile's velocity.
  • A is the projectile's frontal area.
  • ρAir is the density of air.

Solution Approach

Here is my problem attack plan:

  • Load the velocity versus range table into Mathcad
  • Setup up a velocity versus range function that is continuous (i.e. interpolate the data).
  • Use the fact that F_d=m\cdot a=m\cdot \frac{{dv}}{{dt}}=m\cdot \frac{{dv}}{{dx}}\cdot \frac{{dx}}{{dt}}=m\cdot \frac{{dv}}{{dx}}\cdot v to compute the drag force.
  • Compute the drag coefficient as a function of projectile velocity.

Analysis

My goal is to determine just how well I can compute the drag coefficient as a function of velocity from standard velocity versus range tables. You need to understand that my results are approximate, but should give reasonably close answers.

Smoothed Velocity Versus Range Chart

Figure 2 shows how I processed the velocity versus range table to compute drag coefficients.  I am simply performing an interpolation of the velocity-range table.

Figure 2: Generate a Smoothed Version of the Velocity Data.

Figure 2: Generate a Smoothed Version of the Velocity Data.

Generate the Drag Coefficient

In Figure 3, I used my velocity function to

  • compute the projectile's deceleration using a derivative.
  • compute the drag force on the projectile my multiplying the acceleration times the bullet's mass.
  • Substitute the computed drag force into the drag coefficient definition.
Figure 3: Generate a Vector of Drag Coefficients Versus a Velocity Vector.

Figure 3: Generate a Vector of Drag Coefficients Versus a Velocity Vector.

Compare the G7 Coefficients with My Calculations

In Figure 4, I compare the Barnes' G7 drag coefficient data with my calculated drag coefficient. The Barnes' data shows a greater difference in drag coefficient than my calculations. However, my analysis is approximate and I am sure that they have much more complete data than the table I am working with.

FIgure 4: Comparison of Calculated Drag Coefficient Versus G7 Reference.

FIgure 4: Comparison of Calculated Drag Coefficient Versus G7 Reference.

Conclusion

My results are reasonable considering the limited number of data points that I am working with. My plan is to use this tool I have created here to determine just how well the G7 ballistic coefficient matches the performance of projectiles.

Posted in Ballistics | 1 Comment

The Bounty Mutiny and the Pitcairn Island Position Error

Posted on 5-February-2016 by mathscinotes

Quote of the Day

If you want to live a happy life, tie it to a goal, not to people or objects.

— Albert Einstein

Introduction

Figure 1: Pitcairn Island As Seen from the International Space Station.

Figure 1: Pitcairn Island As Seen from the
International Space Station (Source).

I liked reading the book Longitude by Dava Sobel, and I also enjoyed the television movie version.  I was recently doing some reading about the Bounty mutiny when I realized that the problem of measuring longitude played a role in that tale as well.

The story of longitude is one of technology and obsession. While  mariners had been able to measure their latitude accurately for centuries, measuring one's longitude required the development of accurate timepieces. Longitude is the story of the development of the marine chronometer. In essence, our modern GPS systems are extremely accurate clocks that provide the ultimate realization of the longitude goal.

While escaping from Captain Bligh, the Bounty mutineers stumbled upon Pitcairn Island, an island with an actual position that was significantly different than shown on their charts. This error provided the mutineers with an opportunity – the error was so large (181 nautical miles) that their pursuers could only find the island by accident. They decide to make Pitcairn their home and hope that they would remain undiscovered. Their instincts proved to be correct as the Royal Navy would not land on Pitcairn until 1814, which was 25 years after the 1789 mutiny. By then, all but one of the mutineers were dead.

The error was not made by the map's cartographers, but simply reflects the fact that the original discovers did not have an accurate measurement of the island's longitude. Here is an excerpt from log of Captain Pipon of the HMS Tagus, one of two Royal Navy warships that stumbled onto Pitcairn on September of 1814.

On the 17 Sep'r 1811 [1814] at about half past 2 o'clock in the Morning, to my surprise & astonishment, Land was discovered both by the Briton & Tagus & nearly at the same moment. The Ships were hove too, in hailing the Briton, it was determined to continue in that situation until day light in the morning; to ascertain the exact position of the Land in view, & according to circumstances, to reconnoitre it, if necessary. We were then by our reckoning in the Latitude of about 24°..40′ South & Longitude 130°.24W. the Land bearing SSE 5 or 6 leagues. As in all the Charts in our possession there was no Land laid down in, or near this Longitude, we were extremely puzzled to make out what Island it could be; for Pitcairn Island being by all accounts in the Longitude of 133° 24 W . we could not possibly imagine so great an error could have crept in our Charts, with respect to its situation.

This quote shows that the longitude error was over 3° while the latitude error was ~24 arcminutes. Errors of this magnitude were common prior to the development of accurate timepieces. Note that the latitude measurement is much more accurate than the longitude measurement.

Let's examine the charted position versus the actual position (from the Wikipedia) and determine the errors. To keep things simple, I just computed a Euclidean distance, which is close enough for short-ranges on Earth.

Figure 2: My Rough Calculations for the Pitcairn's Charted Position Error.

Figure 2: My Rough Calculations for the Pitcairn's Charted Position Error.

Trying to find a tiny island (18 square miles) when you have a position error of nearly 200 nautical miles is a daunting task.

Posted in Naval History, Navigation | Comments Off on The Bounty Mutiny and the Pitcairn Island Position Error

Remakes Improving The "Robinson Crusoe on Mars" Theme

Posted on 3-February-2016 by mathscinotes

Quote of the Day

If you don't like change, you'll like irrelevance even less.

— General Eric Shinseki, Chief of Staff, U.S. Army. Change is inevitable, and we need to learn to embrace it.

Figure 1: Advertising for the move "The Martian".Figure 1: Advertising for the move "The Martian".Figure 1: Advertising for the move "The Martian".

Figure 1: Advertising for the move "The Martian".

I just watched the movie The Martian with my oldest son, and I really enjoyed it (Figure 1). As I thought about the movie, it certainly was the best of the "man versus Mars" movies I have seen – and it was the first with a real sense of humor. Every so often, Hollywood rediscovers the "escape from Mars" theme and The Martian is the best of this genre yet.

As a boy in 1964, I loved seeing the movie Robinson Crusoe on Mars (RCOM, Figure 2). Both The Martian and RCOM are about a isolated individual trying to survive on Mars until he can be rescued. I consider RCOM to be the last of the 1950s-style science fiction films. Its director was Byron Haskins, who directed the science fiction classic War of the Worlds and would later direct the first Star Trek pilot called "The Cage". I consider "The Cage" to be one of the best science fiction episodes ever produced for television. Unfortunately, Haskins also directed the stinker Conquest of Space. Even the best directors have a few clinkers – remember that George Lucas produced Howard the Duck.

Figure 2: Movie Image from "Robinson Crusoe on Mars".

Figure 2: Movie Image from "Robinson Crusoe on Mars".

In 2000, Hollywood gave us a pair of movies about rescuing astronauts stranded on Mars: Mission to Mars (Figure 3), which has a plot similar  to that of The Martian; Red Planet (Figure 4), a rather messy affair about astronauts trying to escape Mars while being attacked by a wacko robot. Between these two movies, I would take Mission to Mars any day. The characters in Red Planet seem way too macho for a team of techie astronauts.

Figure 4: Mission to Mars Poster.

Figure 3: Mission to Mars Poster (Source).

Figure 3: Red Planet Movie Poster.

Figure 4: Red Planet Movie Poster (Source).
Posted in Personal | Comments Off on Remakes Improving The "Robinson Crusoe on Mars" Theme

Estimating The Lifetime of an Electrolytic Capacitor

Posted on 2-February-2016 by mathscinotes

Quote of the Day

A good stack of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one.

— Paul Halmos

Introduction

Figure 1: Examples of Electrolytic Capacitors that Failed Because of Outgassing.

Figure 1: Examples of Electrolytic Capacitors
that Failed Because of Outgassing.

Our optical products are powered by AC power converters (e.g. wall adapters, uninterruptible power sources) that we buy from outside sources. Over the last two weeks, I have been dealing with a number of aluminum electrolytic capacitor failures in these power products. Like all components, electrolytic capacitors eventually do wear-out (e.g. Figure 1). Unfortunately, their lives are relatively short (~15 years) compared to other components in the system. We have had some of these power sources in the field for nearly ten years, so we are starting to see some worn-out capacitors.

In this post, I will discuss how we predict the lifetime of aluminum electrolytic capacitors in real applications. Unlike most digital components, electrolytic capacitor lifetimes vary markedly based on the level of stress that the power converter designer chooses to impose upon them.

Background

Vendor Reliability Material

Here are the vendor materials upon which I based this post:

Each of the models presented are similar but slightly different. You need to adjust your model based on the vendor parts you are using. In this post, I will be using Jianghai for my reference example.

Definitions

Rated Lifetime (symbol L0)
The nominal lifetime of the capacitor when operated at its rated ripple current, rated operating temperature, and limited voltage stress (i.e. applied voltage less than half the rated voltage). The rated lifetime is measured by the capacitor's manufacturer during stress testing and is usually shorter than the capacitor's lifetime in an application.
Predicted Lifetime (symbol L)
The predicted lifetime of the capacitor in a specific application. In most applications, the predicted lifetime is longer than the rated lifetime because applications usually do not operate at the maximum rated temperature, voltage, and ripple current.
Equivalent Series Resistance (symbol RESR)
Equivalent series resistance causes heat generation within the capacitor when AC ripple current flows through the capacitor. Maximum ESR is normally specified at 120Hz, 20°C.
Applied Ripple Current (symbol IA)
The applied ripple current is the Root-Mean-Square (RMS) value of alternating current flowing through a capacitor. This current causes an internal temperature rise because of the power generated in the ESR of the capacitor.
Rated Ripple Current (symbol IR)
The ripple current at which the vendor specifies L0.

Approach

The basic modeling approach can be described as follows:

  • The capacitor is subjected to two stresses:
    • The temperature within the capacitor.

      The temperature within the capacitor is driven by (1) the ambient temperature of the capacitor, and (2) the power dissipated within the capacitor. Because we cannot directly measure the internal temperature of the capacitor, the capacitor vendors provide ways of estimating the internal temperature rise within the capacitor. Most vendors assume that the lifetime of a capacitor doubles for every 10 °C decrease in internal capacitor temperature, which I will assume here.

    • The voltage applied to the capacitor.

      Every vendor models the lifetime impact of the voltage applied to a capacitor using a power law of the form \left(\frac{V_A}{V_R}\right)^{-n}, where Va is the applied voltage and Vr is the rated voltage. However, the vendors do not all agree on the value of n that should be used, and n must be adjusted for each vendor.

  • We predict the internal temperature by using the ambient temperature of the air around the capacitor plus the internal temperature rise caused by the ripple current passing through RESR.
  • There are different ways to model the amount of internal temperature rise for a given ripple current.
    • The manufacturer will state an internal temperature rise value (e.g. ΔT = 5°C in my example below) at the rated ripple current IR. We can then scale this temperature for the application's ripple current IA.
    • The manufacturer will specify a parameter that relates ambient temperature and capacitor case temperature to the core temperature (e.g. 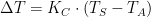\Delta T={{K}_{C}}\cdot \left( {{{T}_{S}}-{{T}_{A}}} \right), where KC is our conversion parameter, TS is the capacitor's surface (i.e. case) temperature, and TA is the ambient temperature. This approach requires measuring the capacitor's case temperature.
    • The manufacturer will specify a thermal resistance (e.g. Θ) or thermal parameter (e.g. Ψ) that relates the power dissipated by the ripple current in the capacitor (i.e. I_{A}^2\cdot R_{ESR}) to the internal temperature rise ΔT.

Standard Model

My preferred form for the capacitor lifetime equation is shown in Equation 1. There are numerous different ways to express this equation, but they are all algebraically equivalent. This model assumes that power losses within the capacitor due to leakage are negligible.

Eq. 1
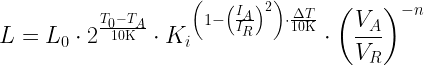
\displaystyle L={{L}_{0}}\cdot {{2}^{{\frac{{{{T}_{0}}-{{T}_{A}}}}{{10\text{K}}}}}}\cdot {{K}_{i}}^{{\left( {1-{{{\left( {\frac{{{{I}_{A}}}}{{{{I}_{R}}}}} \right)}}^{2}}} \right)\cdot \frac{{\Delta T}}{{10\text{K}}}}}\cdot {{\left( {\frac{{{{V}_{A}}}}{{{{V}_{R}}}}} \right)}^{{-n}}}

where

  • L0 is capacitor lifetime when operating at maximum temperature, ripple current, and a specific voltage.
  • T0 is maximum operating temperature.
  • TI is capacitor internal temperature, which I normally estimate using the equation 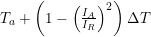{{T}_{a}}+\left( {1-{{{\left( {\frac{{{{I}_{A}}}}{{{{I}_{R}}}}} \right)}}^{2}}} \right)\Delta T. There are other ways to estimate the internal capacitor temperature, but this is the approach I will use for this post.
  • ΔT is the internal temperature rise over the capacitor's case temperature at the rated ripple current IR. The vendors often state the anticipated ΔT when operating at a ripple current of IR. I usually see ΔT value of 5 °C or 15 °C.
  • n is a lifetime modeling parameter that varies by vendor. For the lifetime example that I work in this post, I will assume that n =0 for VA/VR < 0.5 and n = 2.5 otherwise.
  • Ki is a lifetime modeling constant. For the lifetime example that I work in this post, I will assume that Ki = 4 when the IA/IR > 1 and the capacitor temperature is at its max (T0 = 105 °C in this case), otherwise Ki = 2.

I should note that the term 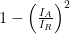{1-{{{\left( {\frac{{{{I}_{A}}}}{{{{I}_{R}}}}} \right)}}^{2}}} will change sign when IA/IR > 1. Instead of acting as a lifetime multiplier, this term now begins to decrease the lifetime of the capacitor. This means that exceeding the rated ripple current specification on an electrolytic capacitor is a very bad thing to do.

I do spend a bit more time on Equation 1 in the Appendix.

Analysis

Objective

My plan here is use Equation 1 to plot L/L0 as a function of IA/IR and TA, which will duplicate the graphic shown in Figure 2 (Source).

Figure 2: Graphic of Capacitor Lifetime Multipliers.

Figure 2: Graphic of Capacitor Lifetime Multipliers.

Graphic Generation

I captured Equation 1 using Mathcad and plotted it assuming that:

  • VA/VR = 1.
  • ΔT = 5 °C, which is specified for the CD 297 BB series capacitor when TA = 105°C  and  IA/IR = 1.

I will vary TA and the IA/IR to generate the contours shown in Figure 3.

Figure 3: Calculations in Mathcad.

Figure 3: Calculations in Mathcad.

Figure 4 show my plot. It is very similar to Figure 2.

Figure 4: My Version of the Lifetime Multiplier Graph.

Figure 4: My Version of the Lifetime Multiplier Graph.

Conclusion

I regularly receive questions from other engineers on how to model the lifetime of electrolytic capacitors. I hope this worked example provides a useful reference.

Appendix A: A More Detailed Look at Equation 1.

Figure 5 shows a more detailed derivation of Equation 1. In typical applications (i.e. current below rated and voltage below rated), Equation 1 can be derived using the Arrhenius relationship and the power-law voltage stress model. When operating at maximum temperature and with ripple currents above the rating value, the term exponent base of 2 changes to 4. I have never used a capacitor with that level of stress.

Figure M: A Detailed Derivation of Equation 1.

Figure 5: A Detailed Derivation of Equation 1.

Posted in Electronics | 1 Comment

Mathcad Solution To XKCD Problem

Posted on 29-January-2016 by mathscinotes

Quote of the Day

I don't need time – I need a deadline.

— Duke Ellington, describing how he is motivated to get something done. I must admit that I need deadlines for writing, otherwise I would never get anything written.

Introduction

Figure 1: Velociraptor Vs Prey Problem Statement (Source).

Figure 1: Velociraptor Vs Prey Problem Statement (Source).

XKCD is a great comic strip by Randall Munroe that takes a quirky look at the world of science. Randall recently posted a set of questions for a substitute teacher to pose to a math class that were interesting and attracted the attention of some problem-solving enthusiasts.

I thought I would jump into the fray by solving the problem using Mathcad and also taking my first dive into Python.

Background

While this is a simple problem, it is interesting to see how different people approach it. Here are two other solutions that I recommend you read:

  • Jon Peltier's Excel Solution

    Jon is a world-class Excel expert (e.g. MVP) with a real gift for Excel charting. He attacks the problem using a standard spreadsheet approach and a Visual Basic for Applications (VBA) approach.

  • Rhett Allain's Python Solution

    Rhett wrote a Python-based solution that I used as the basis for my first Python program. I modified his routine to use trapezoidal integration instead of Euler, and I implemented a different scheme for the clipping the velocities.

Analysis

Mathcad Solution

Figure 2 shows how I used Mathcad to solve the substitute teacher problem.

Figure M: Mathcad Solution to XKCD Problem.

Figure 2: Mathcad Solution to XKCD Problem.

Figure 3 shows my graphical view of the solution.

Figure M: Plot of Raptor Versus Prey.

Figure 3: Plot of Raptor Versus Prey.

Python Solution

I have never written a Python program before and this seemed like a great opportunity to learn. When I looked at Rhett's program, it reminded me a simplified form of Java – my usual programming language choice. So I quick ran through the Python course on Code Academy and loaded Python onto my Eclipse install.

Figure 4 shows my Python routine, which gave me the same results as Mathcad. Python seems a lot less wordy than Java – what were the Java folks thinking?

import matplotlib.pyplot as plt
#!/usr/bin/env python
"""
Abstract: 
This module iteratively solves the xkcd substitute teacher problem:

    The velociraptor spots you 40 meters away and attacks, accelerating
    at 4 m/s^2 up to its top speed of 25 m/s. When it spots you, you 
    begin to flee, quickly reaching your top speed of 6 m/s. How far can
    you get before you are devoured.

My intent here is to solve the problem with a simple Python program. My 
approach here is a slightly modified version of Rhett Allain's Python code 
at http://www.wired.com/2015/10/heres-solve-xkcd-velociraptor-problem-code/
My modifications are simple. 
1. I used trapezoidal rule rather than Euler method for the ODE solution. 
2. I decided to store the intermediate results in lists.
3. Implemented the clipped velocities using minimum function.

Rhett assumes that a prey will accelerate at 3 m/s^2 on their way to a top
speed of 6 m/s, so I will too.
"""
# Initial Conditions
xv=-40      #this is the initial location of velociraptor
xp=0        #location of the prey
av=4        #acceleration of velociraptor
ap=3        #accel of prey 
vvmax=25    #maximum velocity of the velociraptor
vpmax=6     #max velocity of prey
vp=0        #starting velocity of prey
vv=0        #starting velocity of velociraptor
t=0         #starting time
dt=0.0001   #time step
tlist=[]                #Store all time values computed
xpreylist=[]            #Store all prey positions
xvelociraptorlist=[]    #Store all raptor positions

#this is the loop. It runs until the velociraptor
#catches up to the prey
while xv<=xp:#first check if the prey is at max v
   
    #calc new prey velocity after time interval
    vp0=vp
    vp=min(vp+ap*dt,vpmax)
  
    #calc new velociraptor velocity
    vv0=vv
    vv=min(vv+av*dt,vvmax)
    
    #calc new positions
    xp=xp+(vp+vp0)*0.5*dt   #Trapezoidal integration
    xpreylist.insert(0,xp)
    xv=xv+(vv+vv0)*0.5*dt   #Trapezoidal integration
    xvelociraptorlist.insert(0,xv)
    tlist.insert(0,t)
    #update time
    t=t+dt

print 'Prey Position @ intercept time: {0:4}'.format(xp)
print 'Intercept Time (s): {0:4}'.format(t)

# Plot the prey and velociraptor positions

plt.plot(tlist,xpreylist)
plt.plot(tlist,xvelociraptorlist)
plt.ylabel('Position (m)')
plt.xlabel('Time (s)')
plt.suptitle('Velociraptor Vs Prey Position', fontsize=20)
plt.show()

Figure 4: My Python Solution for the Substitute Teacher Problem.

Python Graphic Output

Figure 5 shows the output from my Python program. The results are the same as given by Mathcad.

Figure M: Python Plot of Prey and Velociraptor Position.

Figure 5: Python Plot of Prey and Velociraptor Position.

Conclusion

This problem nicely illustrates how different tools can be used to solve a problem. In my case, I tend to use computer-algebra systems, like Mathcad and Mathematica, to experiment with different approaches to solve a problem. I only commit to software when I need more speed or the ability to handle large scale.

Posted in General Mathematics | 2 Comments

My Minnesota Accent

Posted on 24-January-2016 by mathscinotes

Quote of the Day

It's better to do something imperfectly than to do nothing flawlessly.

— Robert Schuller. I have actually known people who altered their life course because they got a "B" in a subject. I have also known people who failed their elementary electromagnetics courses, who then kept on battling, and who later became some of the best RF designers I have met. Even the world's greatest pilot, Chuck Yeager, threw up his first few times flying. People need to understand that nobody starts out on top – they need to give themselves a break.

I am from a small town in Minnesota called Osseo. I had never traveled far from home until I finished my undergraduate work and moved to Ft. Collins, Colorado. When I arrived in Colorado, everyone that I met immediately knew I was from Minnesota – I had no idea that my accent was so strong. After living five years in Colorado, I also developed an ear for accents, and I also could pick out where people were from because everyone in Colorado was from somewhere else.

The following video does a great job showcasing the Minnesota accent. At the end of the video, one of women mentions that alcoholism is a disease. That statement makes fun of the fact that Minnesota is sometimes jokingly referred to as the "Land of 10,000 Treatment Centers." In addition to our 10,000+ lakes, we do have quite a few treatment centers.

I should add that much of the US is going through a major snow storm today. We are familiar with cold and snow here in Minnesota. The following graphics say it all.

SoTrue MinnesotaLife
Posted in Personal | 2 Comments

Relative Sizes in Photographs Can Be Deceiving

Posted on 23-January-2016 by mathscinotes

Quote of the Day

There may be honor among thieves, but there’s none in politicians.

— TE Lawrence, Lawrence of Arabia. Our 2016 presidential election seems doomed to support Lawrence's assertion.

Introduction

Figure 1: Great Photo of the Moon and a Ship.

Figure 1: Great Photo of the Moon and a Ship (Source).

I often see photographs that appear to show objects with different size relationships than we usually see. In Figure 1, for example, we see the Moon as nearly the same size as the sailboat. This happened because the sailboat is some distance from the camera, and its angular extent is comparable to that of the Moon.

These types of photographs are easy to setup and can be useful when you want to control the angular relationships in a photograph. The technique is called forced perspective and has been used in movie making since the beginning. Even today, I often see movies that use force perspective to create the illusion of huge monsters or people. The Lord of the Rings movies made extensive use of forced perspective. The following Youtube video does a good job showing how they setup these scenes.

Background

General Information

There is an abundance of material on how a camera captures angular relationships, so I only provide a few reference links for those who want more details. The following links are very good.

One fact that I will use is that the Moon subtends an angle of ~0.5 °. We can easily determine this value as shown in Figure 2.

Figure 2: Computation of the Angular Extent of the Moon.

Figure 2: Computation of the Angular Extent of the Moon.

Diameter of the Moon Distance to the Moon

Objective

My plan here is to:

  • Provide a qualitative explanation for the seeming distortion of angular sizes in photographs.
  • Show how we can extract some information about the sailboat in the photograph.

Analysis

Angular Relationships

Figure 3 illustrates the basic angular relationships involved. The reason that the ship and the Moon appear to be about the same angular size is because they are roughly the same angular size, which is determined by the object size divided by its distance from the observer.

Fgure 2: Illustration of the Angular Dimensions.

Figure 3: Illustration of the Angular Dimensions.

Sailboat Characteristics

I can use Figure 4 to estimate:

  • The distance from the waterline to the top of the mast.
  • length of the sailboat.

Only the relative values of the numbers in Figure 4 are important  – the specific numbers represent the particular units used by the graphics program I was have.  In the photo, I see that there is a person leaning against the cabin. I will assume that the actual distance from head-to-foot of this leaning person is 5 feet – this is close enough for this kind of exercise.

Figure 3: Measurements.


Figure 4: Measurements.

Knowing the person's height, I can now estimate the size and distance of the sailboat from the camera (Figure 5).

Figure 5: Determination of Sailboat Characteristics.

Figure 5: Determination of Sailboat Characteristics.

Conclusion

I can state the following facts about the sailboat and its position:

  • It is ~1.1 miles from the camera.
  • It is ~45 feet long.
  • It is ~67 feet from the waterline to the top of the mast.

These are all reasonable numbers that would provide a you a beautiful picture of a silhouetted sailboat at sunset.

Postscript

I was just watching the commentary track for the movie Shane, and the movie's assistant producer Ivan Moffat commented that they shot many scenes of the movie using a telephoto lens to make the Grand Teton mountains appear extra large. Here is a scene that is a good example (Figure 6).

Figure M: Cemetery Hill Funeral Scene from Shane.

Figure 6: Cemetery Hill Funeral Scene from Shane.

Posted in optics | Comments Off on Relative Sizes in Photographs Can Be Deceiving

Computing List Price from BOM Cost

Posted on 21-January-2016 by mathscinotes

Quote of the Day

Not everyone can be a great chef, but a great chef can come from anywhere.

— Ratatouille. This quote is true for every profession.

Introduction

Figure 1: Relationship of Various Product Costs.

Figure 1: Relationship of Various Product Costs.
I know its too busy, but this "cheat sheet" helps
me keep all the terms straight in my head.

All engineers must be familiar with the basics of product costing. In this post, I will cover a common product cost model (Figure 1) and provide two examples that illustrate how to calculate the list price of a product given the product's component costs plus some corporate parameters, like average discount rate and required gross margin.

All product cost models are related, but they differ in the details. The model shown in Figure 1 is a common one, but I certainly have used others. This particular model is similar to that used by my son's firm.

The key lesson of this exercise is to show that every dollar spent on components ends up contributing multiple dollars to the list price. This is why I focus so intensely on ensuring that every component pulls its weight in terms of delivering value to customers. To my engineers, I often quote Andrew Carnegie, who is famous for saying "Control costs and profits will follow."

For financial work, I usually use Excel. However, this exercise did involve solving a system of equations, so I used Mathcad. I then used my Mathcad results to check an Excel spreadsheet I cooked up for general use (available here).

Background

Definitions of Cost Elements

Bill of Materials (BOM) Cost (symbol CBOM)
The cost of the individual components that make up an assembly. This cost is driven by the product requirements and the implementation approach used by the design engineers. In general, standard component costs are assumed – standard costs are a baseline set for each component each quarter. Any component cost variances from the standard are accounted for in OCOGS.
Assembly Cost (symbol CAsm)
The cost of assembling the components into a product. This cost does not include the freight charge associated with shipping the product from the manufacturing site to a distribution center.
Final Cost (symbol CFinal)
This is a non-standard nomenclature. It is simply the sum of the BOM cost and assembly cost.
Freight Cost (symbol CFreight)
Cost of shipping the product to a distribution center. This cost is highly variable because it depends on how you package the product (e.g. one per box, multiple per box), the distance shipped, and the mode of transportation (e.g. airplane versus container ship).
Standard Cost of Goods Sold (symbol SCOGS)
The sum of the final cost and freight.
Other Cost of Goods Sold (symbol OCOGS)
Sometimes issues arise in manufacturing a product that results in variances in our BOM cost from the standard. These variances include things like purchase part variances (i.e. unexpected part cost changes from the standard), excess and obsolete charges, and expedite fees.
Cost of Goods Sold (symbol COGS)
COGS is the cost of creating the products that a company sells – it only includes those costs that are directly tied to the production of the product.
Average Sales Price (ASP)
The average price for which the product was sold. This number is important because it is used to compute revenue R, i.e. R=ASP\cdot N, where N is the number of units sold.
List Price (symbol LP)
The advertised price of a product.

Definitions of Corporate Parameters

Gross Margin Percentage (symbol GM%)
The percentage of profit in the ASP. GM% relates COGS to ASP using the equation COGS=\left( {1-GM\%} \right)\cdot ASP.
OCOGS Percentage (symbol OCOGS%is)
The percentage of OCOGS in the ASP. OCOGS% relates OCOGS to ASP using the equation OCOGS=OCOGS\%\cdot ASP.
Conversion Cost Percentage (symbol CC%)
The assembly cost percentage in the final cost. Because freight varies with distance and mode of shipment, CC% never includes freight cost to ensure that assembly rates can be directly compared. CC% is used to compute assembly cost using the equation {{C}_{{Asm}}}=\frac{{CC\%}}{{1-CC\%}}\cdot {{C}_{{BOM}}}.
Discount (symbol D%)
The average discount received by customers. Discount is used to relate LP to ASP through the equation ASP=\left( {1-D\%} \right)\cdot LP.

Objective

My plan here is to show how to compute the list price of a mythical product with a total component cost of $100. All the corporate parameters I will be assuming are similarly mythical.

Analysis

Approach

With the exception of OCOGS – which is a function of SCOGS, OCOGS%, and GM% – all the equations are straightforward and given in the definitions above. I derive an equation for OCOGS in Figure 2.

Figure M: Derivation of OCOG equation.

Figure 2: Derivation of OCOGS equation.

Example: Compute List Price Given BOM Cost

Figure 3 show how you can compute the list price of a product given the BOM cost, freight cost, and the corporate parameters.

Figure M: Calculation of List Price from BOM Cost.

Figure 3: Calculation of List Price from BOM Cost.

Example: Compute BOM Cost Given List Price

Figure 4 show how you can compute the BOM cost of a product given the list price, freight cost, and the corporate parameters. This example is the reverse of the example in Figure 3.

Figure 4: Example Computing BOM Cost Given List Price.

Figure 4: Example Computing BOM Cost Given List Price.

Conclusion

In this example, a $1 of BOM cost converts to nearly $3 of list price. This is not an unusual ratio. For example, when I worked at HP in the 80's, $1 of BOM cost converted to $4 of list price.

I have wanted to prepare a costing/pricing calculation example for some time – I finally got around to it. The math is not difficult – you just need to keep things organized.

Posted in Financial | Comments Off on Computing List Price from BOM Cost